Cho hàm số $f\left( x \right) = \ln x.$ Tính đạo hàm của hàm số $g\left( x \right) = {\log _3}\left( {{x^2}f'\left( x \right)} \right).$
Ta có $f'\left( x \right) = \dfrac{1}{x}$$ \Rightarrow g\left( x \right) = {\log _3}\left( {{x^2}.f'\left( x \right)} \right) = {\log _3}\left( {{x^2}.\dfrac{1}{x}} \right) = {\log _3}x$
Suy ra $g'\left( x \right) = \dfrac{1}{{x\ln 3}}.$
Ta có $f'\left( x \right) = \dfrac{1}{x}$$ \Rightarrow g\left( x \right) = {\log _3}\left( {{x^2}.f'\left( x \right)} \right) = {\log _3}\left( {{x^2}.\dfrac{1}{x}} \right) = {\log _3}x$
Suy ra $g'\left( x \right) = \dfrac{1}{{x\ln 3}}.$
Tính đạo hàm của hàm số $y = {2^{\ln \left( {{x^2} + 1} \right)}}.$
Ta có $y' = \left[ {\ln \left( {{x^2} + 1} \right)} \right]'{.2^{\ln \left( {{x^2} + 1} \right)}}.\ln 2 = \dfrac{{2x}}{{{x^2} + 1}}{.2^{\ln \left( {{x^2} + 1} \right)}}.\ln 2.$
Tính đạo hàm của hàm số $y = {\ln ^2}\left( {\ln x} \right)$ tại điểm $x = e$.
Ta có:
\(y' = 2\left[ {\ln \left( {\ln x} \right)} \right]'.\ln \left( {\ln x} \right)\)
Mà ${\left[ {\ln \left( {\ln x} \right)} \right]^/} = \dfrac{{{{\left( {\ln x} \right)}^/}}}{{\ln x}} = \dfrac{{\dfrac{1}{x}}}{{\ln x}} = \dfrac{1}{{x\ln x}}.$
Suy ra ${y^/} = 2.\dfrac{1}{{x\ln x}}.\ln \left( {\ln x} \right) = \dfrac{{2\ln \left( {\ln x} \right)}}{{x\ln x}}$ $ \Rightarrow {y^/}\left( e \right) = \dfrac{{2\ln \left( {\ln e} \right)}}{{e.\ln e}} = \dfrac{{2.\ln 1}}{{e.\ln e}} = 0$
Cho \(a\), \(b\), \(c\) dương và khác \(1\). Các hàm số \(y = {\log _a}x\), \(y = {\log _b}x\), \(y = {\log _c}x\) có đồ thị như hình vẽ. Khẳng định nào dưới đây đúng?
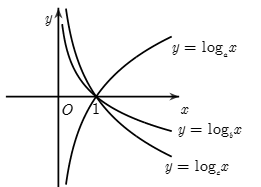
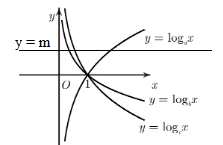
Kẻ đường thẳng \(y = m > 0\) như hình vẽ ta có:
\({\log _a}{x_1} = m \Leftrightarrow {x_1} = {a^m},{\log _b}{x_2} = m \Leftrightarrow {x_2} = {b^m},{\log _c}{x_3} = m \Leftrightarrow {x_3} = {c^m}\)
Quan sát hình vẽ ta thấy \({x_2} < {x_3} < {x_1} \Leftrightarrow {b^m} < {c^m} < {a^m}\).
Mà \(m > 0\) nên \(b < c < a\) hay \(a > c > b\).
Cho hàm số $f\left( x \right) = 4\ln \left( {\sqrt {x - 4} + \sqrt x } \right) + \sqrt {{x^2} - 4x} $ với $x \ge 4$. Tính giá trị của biểu thức $P = f\left( 4 \right) - {\left[ {f'\left( 8 \right)} \right]^2}.\ln 2.$
Ta có $f'\left( x \right) = 4.\dfrac{{\left( {\sqrt {x - 4} + \sqrt x } \right)'}}{{\sqrt {x - 4} + \sqrt x }} + \dfrac{{x - 2}}{{\sqrt {{x^2} - 4x} }} = \dfrac{x}{{\sqrt {{x^2} - 4x} }}$.
Khi đó $f'\left( 8 \right) = \sqrt 2 $ và $f\left( 4 \right) = 4\ln 2$.
Vậy $P = f\left( 4 \right) - {\left[ {f'\left( 8 \right)} \right]^2}.\ln 2 = 4\ln 2 - {\left( {\sqrt 2 } \right)^2}.\ln 2 = 2.\ln 2$.
Cho \(a,{\rm{ }}b\) là hai số thực thỏa mãn \({a^{\dfrac{{\sqrt 3 }}{3}}} > {a^{\dfrac{{\sqrt 2 }}{2}}}\)và \({\log _b}\dfrac{3}{4} < {\log _b}\dfrac{4}{5}\). Mệnh đề nào sau đây là đúng?
Ta có \(\dfrac{{\sqrt 3 }}{3} < \dfrac{{\sqrt 2 }}{2}\), mà \({a^{\dfrac{{\sqrt 3 }}{3}}} > {a^{\dfrac{{\sqrt 2 }}{2}}}\).
Suy ra hàm đặc trưng \(y = {a^x}\) nghịch biến nên \(0 < a < 1\).
Tượng tự có \(\dfrac{3}{4} < \dfrac{4}{5}\) và \({\log _b}\dfrac{3}{4} < {\log _b}\dfrac{4}{5}\).
Suy ra hàm đặc trưng \(y = {\log _b}x\) đồng biến nên \(b > 1\).
Vậy \(0 < a < 1\) và \(b > 1\).
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
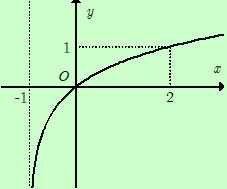
Dựa vào đồ thị thấy có tiệm cận đứng \(x = - 1\). Loại đáp án A, C.
Đồ thị hàm số đi qua điểm có tọa độ \(\left( {2;1} \right)\) nên chỉ có D thỏa mãn
Cho hàm số \(y = \ln x\) có đồ thị như Hình \(1\). Đồ thị Hình \(2\) là của hàm số nào dưới đây?
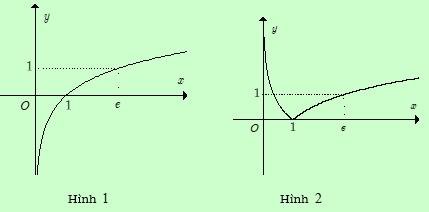
Đồ thị Hình 2 được suy ra từ đồ thị Hình 1 bằng cách:
+ Giữ nguyên phần \(y \ge 0.\)
+ Lấy đối xứng qua \(Ox\) phần \(y < 0.\)
Cho hàm số $y = {5^x}$ có đồ thị $\left( C \right).$ Hàm số nào sau đây có đồ thị đối xứng với $\left( C \right)$ qua đường thẳng $y = x.$
Đồ thị hàm số \(y = {5^x}\) đối xứng với đồ thị hàm số \(y = {\log _5}x\) qua đường thẳng \(y = x\).
Cho hàm số $y = - {\log _2}x$ có đồ thị $\left( C \right).$ Hàm số nào sau đây có đồ thị đối xứng với $\left( C \right)$ qua đường thẳng $y = x.$
Trước tiên ta đưa hàm số về dạng chuẩn: $y = - {\log _2}x = {\log _{{2^{ - 1}}}}x = {\log _{\frac{1}{2}}}x$.
Suy ra hàm số cần tìm là \(y = {\left( {\dfrac{1}{2}} \right)^x} = {2^{ - x}}.\)
Đối xứng qua trục hoành của đồ thị hàm số $y = {\log _2}x$ là đồ thị nào trong các đồ thị có phương trình sau đây?
Dựa vào lý thuyết \(''\)Đồ thị hàm số \(y = f\left( x \right)\) đối xứng qua trục hoành ta được đồ thị hàm số \(y = - f\left( x \right)\)\(''\).
Do đó đồ thị hàm số $y = {\log _2}x$ đối xứng qua trục hoành ta được đồ thị hàm số $y = - {\log _2}x = {\log _{{2^{ - 1}}}}x = {\log _{\dfrac{1}{2}}}x$
Cho $a,{\rm{ }}b,{\rm{ }}c$ là các số thực dương khác $1$. Hình vẽ bên là đồ thị của ba hàm số \(y = {\log _a}x\), \(y = {\log _b}x\), \(y = {\log _c}x\). Khẳng định nào sau đây là đúng?
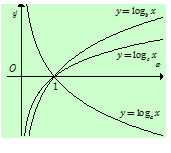
Ta thấy hàm \(y = {\log _a}x\) có đồ thị từ trái sang phải theo hướng đi xuống nên là hàm nghịch biến hay \(0 < a < 1.\)
Còn hàm số \(y = {\log _b}x\) và \(y = {\log _c}x\) là những hàm đồng biến \( \Rightarrow b,{\rm{ }}c > 1.\)
Từ đó loại được các đáp án C, D.
Từ đồ thị hàm số ta thấy tại cùng một giá trị ${x_0} > 1$ thì đồ thị hàm số \(y = {\log _b}x\) nằm trên đồ thị hàm số \(y = {\log _c}x\) hay \(\left\{ \begin{array}{l}x > 1\\{\log _b}x > {\log _c}x\end{array} \right. \Rightarrow b < c\).
Vậy $a < b < c.$
Cho hàm số $y = {3^{\frac{x}{2}}}$ có đồ thị $\left( C \right).$ Hàm số nào sau đây có đồ thị đối xứng với $\left( C \right)$ qua đường thẳng $y = x.$
Trước tiên ta đưa hàm số về dạng chuẩn: $y = {3^{\frac{x}{2}}} = {\left( {\sqrt 3 } \right)^x}$.
Dựa vào lý thuyết \(''\)Hai hàm số $y = {a^x}$ và $y = {\log _a}x$ có đồ thị đối xứng nhau qua đường phân giác của góc phần tư thứ nhất $y = x''$.
Khi đó đồ thị hàm số \(y = {\left( {\sqrt 3 } \right)^x}\) đối xứng với đồ thị hàm số \(y = {\log _{\sqrt 3 }}x = 2{\log _3}x\) qua đường thẳng \(y = x\)
Hàm số \(y = {\log _a}x\) có đạo hàm là:
Điều kiện xác định: $x>0$
Đạo hàm hàm số \(y = {\log _a}x\) là \(y' = \dfrac{1}{{x\ln a}}\)
Hàm số \(f\left( x \right) = {\log _2}\left( {{x^2} - 2x} \right)\) có đạo hàm:
Sử dụng công thức tính đạo hàm của hàm hợp ta được:
\(f'\left( x \right) = \left[ {{{\log }_2}\left( {{x^2} - 2x} \right)} \right]' = \dfrac{{\left( {{x^2} - 2x} \right)'}}{{\left( {{x^2} - 2x} \right)\ln 2}} = \dfrac{{2x - 2}}{{\left( {{x^2} - 2x} \right)\ln 2}}.\)
Cho các hàm số \(y = {a^x};y = {\log _b}x;y = {\log _c}x\) có đồ thị như hình vẽ.
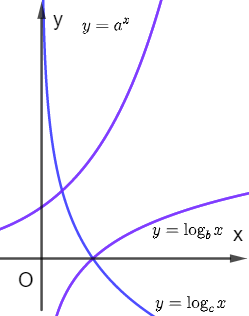
Chọn mệnh đề đúng?
Bước 1: Sử dụng tính đồng biến nghịch biến của hàm số mũ và logarit để so sánh a, b, c với 0 và 1.
Từ các đồ thị hàm số, ta thấy \(y = {a^x}\) và \(y = {\log _b}x\) là các hàm số đồng biến nên \(a > 1\) và \(b > 1\).
Mặt khác, \(y = {\log _c}x\) là hàm số nghịch biến nên \(0 < c < 1\).
Như thế c sẽ nhỏ hơn a và b.
Bước 2: Vẽ đồ thị hàm số \(y = {\log _a}x\) . Kẻ đường thẳng \(y = 1\) từ đó so sánh a với b.
Vẽ đồ thị hàm số \(y = {\log _a}x\) bằng cách lấy đối xứng đồ thị hàm số \(y = {a^x}\) qua đường thẳng \(y = x\).
Kẻ đường thẳng \(y = 1\) cắt hai đồ thị hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) lần lượt tại hai điểm \(A\) và \(B\). Khi đó, \({x_A} = a\) và \({x_B} = b\).
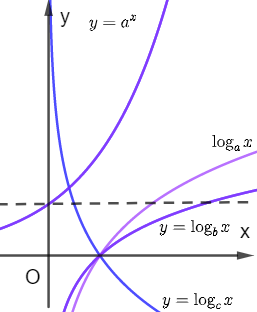
Từ đồ thị hàm số ta thấy \({x_A} < {x_B}\). Vậy \(a < b\).
Vậy c<a<b
Khẳng định nào dưới đây là sai khi nói về hàm số \(y = {\log _a}x\) (với \(0 < a \ne 1\))
Hàm số \(y = {\log _a}x\,\,\,\left( {0 < a \ne 1} \right)\)
+ TXĐ : \(\left( {0; + \infty } \right)\) nên C sai
+ Đồng biến trên \(\left( {0; + \infty } \right)\) nếu \(a > 1\) và nghịch biến trên \(\left( {0; + \infty } \right)\) nếu \(0 < a < 1\) nên A đúng
+ Đồ thị hàm số có một tiệm cận đứng là \(x = 0\) và không có tiệm cận ngang nên B đúng
+ Đồ thị hàm số luôn nằm bên phải trục tung nên D đúng.
Đạo hàm của hàm số \(y = {\log _3}\left( {{x^2} + 1} \right)\) tại điểm \(x = 1\) bằng:
Ta có \(y = {\log _3}\left( {{x^2} + 1} \right) \Rightarrow y' = \frac{{2x}}{{\left( {{x^2} + 1} \right)\ln 3}}\)\( \Rightarrow y'\left( 1 \right) = \frac{1}{{\ln 3}}\).
Tính đạo hàm của hàm số \(y = {\log _2}\left| {5x + 1} \right|\).
ĐK: \(x \ne - \dfrac{1}{5}\)
\(\begin{array}{l}y = {\log _2}\left| {5x + 1} \right| = \left\{ \begin{array}{l}{\log _2}\left( {5x + 1} \right)khix > - \dfrac{1}{5}\\{\log _2}\left( { - 5x - 1} \right)khix < - \dfrac{1}{5}\end{array} \right.\\ \Rightarrow y' = \left\{ \begin{array}{l}\dfrac{5}{{\left( {5x + 1} \right)\ln 2}},\,khix > - \dfrac{1}{5}\\\dfrac{{ - 5}}{{\left( { - 5x - 1} \right)\ln 2}},\,khi x < - \dfrac{1}{5}\end{array} \right.\\ = \dfrac{5}{{\left( {5x + 1} \right)\ln 2}}\, khi x \ne - \dfrac{1}{5}\end{array}\)
Trên khoảng \(\left( {0; + \infty } \right)\), hàm số \(y = {\log _3}x\) có đạo hàm là:
\(y = {\log _3}x\) \( \Rightarrow y' = \dfrac{1}{{x\ln 3}}\).

