Tìm tập xác định của hàm số \(y = {e^{\log \left( { - {x^2} + 3x} \right)}}.\)
Hàm số \(y = {e^{\log \left( { - {x^2} + 3x} \right)}}\) xác định \( \Leftrightarrow - {x^2} + 3x > 0\)\( \Leftrightarrow x\left( {x - 3} \right) < 0\)\( \Leftrightarrow 0 < x < 3\)
Tập xác định của hàm số \(y = 3{x^2} + 4x - 3\sqrt {{{\log }_2}\left( {x + 4} \right)} \) là:
ĐKXĐ: \(\left\{ \begin{array}{l}x + 4 > 0\\{\log _2}\left( {x + 4} \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 4\\x + 4 \ge 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 4\\x \ge - 3\end{array} \right. \Leftrightarrow x \ge - 3.\)
Vậy TXĐ của hàm số là \(D = \left[ { - 3; + \infty } \right)\).
Tìm số các giá trị nguyên không dương của tham số \(m\) để hàm số \(y = \dfrac{{m\ln x - 2}}{{\ln x + m - 3}}\) đồng biến trên \(\left( {{e^2}; + \infty } \right)\) là
Đặt \(t = \ln x,\,\,\,t \in \mathbb{R}.\) Hàm số đã cho trở thành \(y = \dfrac{{mt - 2}}{{t + m - 3}}\,\,\,\left( {t \ne 3 - m} \right)\) (1)
Xét hàm số \(t = \ln x\) với\(x \in \left( {{e^2}; + \infty } \right)\)ta có: \(t'\left( x \right) = \dfrac{1}{x} > 0\,\,\forall x \in \left( {{e^2}; + \infty } \right)\).
Do đó hàm số \(t = \ln x\) đồng biến trên khoảng \(\left( {{e^2}; + \infty } \right)\), do đó ta có: \(t \in \left( {2; + \infty } \right)\).
Yêu cầu bài toán trở thành : Tìm số các giá trị nguyên không dương của tham số \(m\) để hàm số \(y = f\left( t \right) = \dfrac{{mt - 2}}{{t + m - 3}}\) đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
Ta có: \(f'\left( t \right) = \dfrac{{m\left( {m - 3} \right) + 2}}{{{{\left( {t + m - 3} \right)}^2}}} = \dfrac{{{m^2} - 3m + 2}}{{{{\left( {t + m - 3} \right)}^2}}}.\)
Hàm số \(y = f\left( t \right)\) đồng biến trên khoảng \(\left( {2; + \infty } \right)\) khi nó xác định trên khoảng \(\left( {2; + \infty } \right)\) đồng thời \(f'\left( t \right) \ge 0,\,\,\,\forall t \in \left( {2; + \infty } \right)\) (Dấu ‘=’ chỉ xảy ra tại một số hữu hạn điểm).
Do đó, \(\left\{ \begin{array}{l}t \ne 3 - m\,\,\forall t \in \left( {2; + \infty } \right)\\{m^2} - 3m + 2 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3 - m \le 2\\\left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ge 1\\\left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\end{array} \right. \Leftrightarrow m > 2.\)
Suy ra không có giá trị nguyên không dương nào của \(m\) thỏa mãn yêu cầu bài toán.
Cho hàm số \(y = \dfrac{1}{{x + 1 + \ln x}}\) với \(x > 0\). Khi đó \( - \dfrac{{{y’ }}}{{{y^2}}}\) bằng
Ta có \(y = \dfrac{1}{{x + 1 + \ln x}}\)\( \Rightarrow \dfrac{1}{y} = x + 1 + \ln x\)
\( \Rightarrow {\left( {\dfrac{1}{y}} \right)^\prime } = {(x + 1 + \ln x)^\prime }\)\( \Leftrightarrow - \dfrac{{{y^\prime }}}{{{y^2}}} = 1 + \dfrac{1}{x}\)
Hàm số nào sau đây nghịch biến trên khoảng xác định của nó?
Hàm số \(y = {\log _{\dfrac{1}{2}}}x\) nghịch biến trên khoảng xác định của nó, do \(0 < \dfrac{1}{2} < 1\).
Tìm tất cả các giá trị thực của tham số m để hàm số: \(y = {\log _3}\left( {{9^x} - {3^x} + m} \right)\) có tập xác định là \(\mathbb{R}\).
ĐKXĐ: \({9^x} - {3^x} + m > 0 \Leftrightarrow m > - {9^x} + {3^x}\)
Để hàm số: \(y = {\log _3}\left( {{9^x} - {3^x} + m} \right)\) có tập xác định là R thì \(m > - {9^x} + {3^x},\forall x \in \mathbb{R}\) (*)
Đặt \(t = {3^x},\,t > 0\), xét hàm số \(f\left( t \right) = - {t^2} + t,\,\left( {t > 0} \right),\,\,f'\left( t \right) = - 2t + 1,\,\,f'\left( t \right) = 0 \Leftrightarrow t = \dfrac{1}{2}\)
BBT:
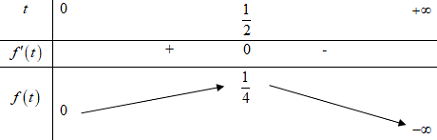
Khi đó, (*) \( \Leftrightarrow m > \dfrac{1}{4}\).
Hàm số \(y = {\log _3}\left( {{x^2} - mx + 2} \right)\) có tập xác định là \(\mathbb{R}\) khi
Hàm số \(y = {\log _3}\left( {{x^2} - mx + 2} \right)\) có tập xác định là \(\mathbb{R}\) khi và chỉ khi
\(\begin{array}{l}{x^2} - mx + 2 > 0\,\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\\Delta = {m^2} - 8 < 0\end{array} \right. \Leftrightarrow - 2\sqrt 2 < m < 2\sqrt 2 .\end{array}\)
Hàm số \(y = {\log _3}\left( {{x^2} - mx + 2} \right)\) có tập xác định là \(\mathbb{R}\)khi
Hàm số \(y = {\log _3}\left( {{x^2} - mx + 2} \right)\) có tập xác định là \(\mathbb{R}\) khi và chỉ khi
\(\begin{array}{l}{x^2} - mx + 2 > 0\,\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\\Delta = {m^2} - 8 < 0\end{array} \right. \Leftrightarrow - 2\sqrt 2 < m < 2\sqrt 2 .\end{array}\)
Tìm tập xác định của hàm số \(y = {\log _x}\left( {5x - 2{x^2} - 2} \right)\)
ĐK :\(\left\{ \begin{array}{l}0 < x \ne 1\\5x - 2{x^2} - 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \ne 1\\\dfrac{1}{2} < x < 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{2} < x < 2\\x \ne 1\end{array} \right.\)
TXĐ : \(D = \left( {\dfrac{1}{2};1} \right) \cup \left( {1;2} \right)\)
Cho hàm số \(y = \dfrac{1}{{x + 1 + \ln x}}\) với \(x > 0\). Khi đó \( - \dfrac{{y'}}{{{y^2}}}\) bằng:
Ta có \(y = \dfrac{1}{{x + 1 + \ln x}} \Rightarrow y' = \dfrac{{ - \left( {1 + \dfrac{1}{x}} \right)}}{{{{\left( {x + 1 + \ln x} \right)}^2}}}\)
Khi đó \( - \dfrac{{y'}}{{{y^2}}} = \dfrac{{1 + \dfrac{1}{x}}}{{{{\left( {x + 1 + \ln x} \right)}^2}}}:\dfrac{1}{{{{\left( {x + 1 + \ln x} \right)}^2}}}\)\( = 1 + \dfrac{1}{x}\)
Cho hàm số \(f\left( x \right) = \ln \left( {{e^x} + \pi m} \right)\) thỏa mãn \(f'\left( {\ln 3} \right) = 3\). Mệnh đề nào sau đây đúng?
\(f\left( x \right) = \ln \left( {{e^x} + \pi m} \right) \Rightarrow f'\left( x \right) = \dfrac{{{e^x}}}{{{e^x} + \pi m}}\)
\(f'\left( {\ln 3} \right) = 3 \Leftrightarrow \dfrac{3}{{3 + \pi m}} = 3 \Leftrightarrow m = - \dfrac{2}{\pi } \approx - 0,64 \in \left( { - 1;0} \right)\)
Cho 3 số thực dương \(a,\,b,\,c\) khác 1. Đồ thị các hàm số \(y = {a^x},\)\(y = {\log _b}x,\)\(y = {\log _c}x\) được cho như trong hình vẽ.
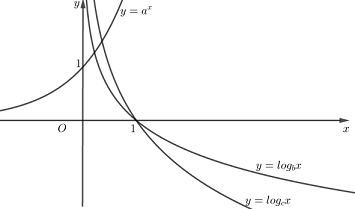
Mệnh đề nào dưới đây là mệnh đề đúng?
Từ đồ thị các hàm số đã cho ta thấy:
Hàm số \(y = {a^x}\) luôn đồng biến trên \(\mathbb{R}\) nên \(a > 1\)
Hàm số \(y = {\log _b}x\) và \(y = {\log _c}x\) luôn nghịch biến trên \(\left( {0; + \infty } \right)\) nên \(0 < b;c < 1\). Mặt khác, với mọi giá trị của \(x\) trong khoảng \(\left( {1; + \infty } \right)\) thì \({\log _b}x > {\log _c}x\) nên \(b < c\)
Do đó \(0 < b < c < 1 < a \Leftrightarrow b < c < a\)
Chọn công thức đúng ?
Áp dụng công thức ta có:
\(\left( {{{\log }_a}x} \right)' = \frac{1}{{x\ln a}}\)(x>0)
\(\begin{array}{l}\left( {\ln 4x} \right)' = \left( {\ln 4 + \ln x} \right)' \\= \left( {\ln 4} \right) '+ \left( {\ln x} \right)' = 0 + \frac{1}{x} \\= \frac{1}{x}\left( {x > 0} \right)\\\left( {\ln x} \right)' = \frac{1}{x}\left( {x > 0} \right)\end{array}\)
Đề thi THPT QG 2020 – mã đề 104
Tập xác định của hàm số \(y = {\log _4}x\) là
Hàm số \(y = {\log _4}x\) xác định \( \Leftrightarrow x > 0.\)
Biết rằng hàm số \(f\left( x \right) = \sqrt x \ln x\) đạt giá trị lớn nhất trên đoạn \(\left[ {1;e} \right]\) tại \(x = {x_0}\). Mệnh đề nào sau đây là đúng?
Hàm số xác định và liên tục trên đoạn \(\left[ {1;e} \right]\).
Đạo hàm \(f'\left( x \right) = \left( {\sqrt x } \right)'.\ln x + \sqrt x .\left( {\ln x} \right)'\)\( = \dfrac{{\ln x}}{{2\sqrt x }} + \dfrac{1}{{\sqrt x }} = \dfrac{{\ln x + 2}}{{2\sqrt x }}\)
Suy ra \(f'\left( x \right) = 0 \Leftrightarrow \ln x + 2 = 0 \Leftrightarrow \ln x = - 2\)\( \Leftrightarrow x = {e^{ - 2}} = \dfrac{1}{{{e^2}}} \notin \left[ {1;e} \right]\)
Ta có \(\left\{ \begin{array}{l}f\left( 1 \right) = 0\\f\left( e \right) = \sqrt e \end{array} \right.\) \( \Rightarrow \mathop {\max }\limits_{\left[ {1;e} \right]} f\left( x \right) = f\left( e \right) = \sqrt e \).
Do đó \(x_0=e\).
Chọn mệnh đề đúng:
Giới hạn cần nhớ: \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\)
Cho hàm số \(y = {\log _a}x\). Nếu \(0 < a < 1\) thì hàm số:
Hàm số \(y = {\log _a}x\) nghịch biến trên \(\left( {0; + \infty } \right)\) nếu \(0 < a < 1\) và đồng biến trên \(\left( {0; + \infty } \right)\) nếu \(a > 1\).
Tiệm cận đứng của đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) là đường thẳng:
Đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đường tiệm cận đứng là \(x = 0\) (trục \(Oy\))
Điểm \(\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) nếu:
Điểm \(\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) nếu \({y_0} = {\log _a}{x_0}\).
Điểm nào sau đây không thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\)?
- Đồ thị hàm số luôn đi qua các điểm \(\left( {1;0} \right)\) và \(\left( {a;1} \right)\).
- Với \(x = {a^2}\) thì \(y = {\log _a}x = {\log _a}{a^2} = 2\) nên đồ thị hàm số đi qua \(\left( {{a^2};2} \right)\) nên C sai, D đúng.

