Câu hỏi:
2 năm trước
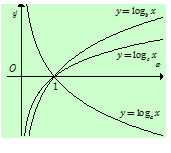
Cho $a,{\rm{ }}b,{\rm{ }}c$ là các số thực dương khác $1$. Hình vẽ bên là đồ thị của ba hàm số \(y = {\log _a}x\), \(y = {\log _b}x\), \(y = {\log _c}x\). Khẳng định nào sau đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: b
Ta thấy hàm \(y = {\log _a}x\) có đồ thị từ trái sang phải theo hướng đi xuống nên là hàm nghịch biến hay \(0 < a < 1.\)
Còn hàm số \(y = {\log _b}x\) và \(y = {\log _c}x\) là những hàm đồng biến \( \Rightarrow b,{\rm{ }}c > 1.\)
Từ đó loại được các đáp án C, D.
Từ đồ thị hàm số ta thấy tại cùng một giá trị ${x_0} > 1$ thì đồ thị hàm số \(y = {\log _b}x\) nằm trên đồ thị hàm số \(y = {\log _c}x\) hay \(\left\{ \begin{array}{l}x > 1\\{\log _b}x > {\log _c}x\end{array} \right. \Rightarrow b < c\).
Vậy $a < b < c.$
Hướng dẫn giải:
- Nhận xét \(a,b,c\) dựa vào tính đồng biến nghịch biến của mỗi hàm số.
- Nhận xét mối quan hệ giữa \(b,c\) dựa vào phần đồ thị trong khoảng \(\left( {1; + \infty } \right)\), phần nào nằm trên thì cơ số nhỏ hơn.
