Câu hỏi:
2 năm trước
Cho \(a\), \(b\), \(c\) dương và khác \(1\). Các hàm số \(y = {\log _a}x\), \(y = {\log _b}x\), \(y = {\log _c}x\) có đồ thị như hình vẽ. Khẳng định nào dưới đây đúng?
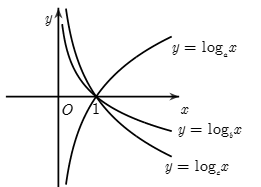
Trả lời bởi giáo viên
Đáp án đúng: c
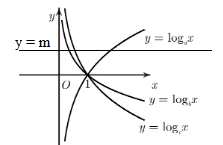
Kẻ đường thẳng \(y = m > 0\) như hình vẽ ta có:
\({\log _a}{x_1} = m \Leftrightarrow {x_1} = {a^m},{\log _b}{x_2} = m \Leftrightarrow {x_2} = {b^m},{\log _c}{x_3} = m \Leftrightarrow {x_3} = {c^m}\)
Quan sát hình vẽ ta thấy \({x_2} < {x_3} < {x_1} \Leftrightarrow {b^m} < {c^m} < {a^m}\).
Mà \(m > 0\) nên \(b < c < a\) hay \(a > c > b\).
Hướng dẫn giải:
Kẻ đường thẳng \(y = m > 0\) và so sánh các giá trị \(a,b,c\).

