Câu hỏi:
2 năm trước
Cho các hàm số \(y = {a^x};y = {\log _b}x;y = {\log _c}x\) có đồ thị như hình vẽ.
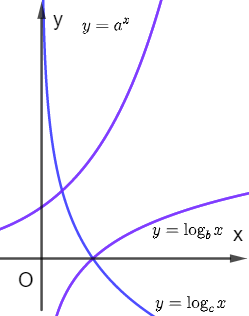
Chọn mệnh đề đúng?
Trả lời bởi giáo viên
Đáp án đúng: d
Bước 1: Sử dụng tính đồng biến nghịch biến của hàm số mũ và logarit để so sánh a, b, c với 0 và 1.
Từ các đồ thị hàm số, ta thấy \(y = {a^x}\) và \(y = {\log _b}x\) là các hàm số đồng biến nên \(a > 1\) và \(b > 1\).
Mặt khác, \(y = {\log _c}x\) là hàm số nghịch biến nên \(0 < c < 1\).
Như thế c sẽ nhỏ hơn a và b.
Bước 2: Vẽ đồ thị hàm số \(y = {\log _a}x\) . Kẻ đường thẳng \(y = 1\) từ đó so sánh a với b.
Vẽ đồ thị hàm số \(y = {\log _a}x\) bằng cách lấy đối xứng đồ thị hàm số \(y = {a^x}\) qua đường thẳng \(y = x\).
Kẻ đường thẳng \(y = 1\) cắt hai đồ thị hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) lần lượt tại hai điểm \(A\) và \(B\). Khi đó, \({x_A} = a\) và \({x_B} = b\).
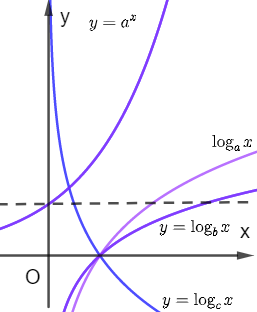
Từ đồ thị hàm số ta thấy \({x_A} < {x_B}\). Vậy \(a < b\).
Vậy c<a<b
Hướng dẫn giải:
Bước 1: Sử dụng tính đồng biến nghịch biến của hàm số mũ và logarit để so sánh a, b, c với 0 và 1.
Bước 2: Vẽ đồ thị hàm số \(y = {\log _a}x\) . Kẻ đường thẳng \(y = 1\) từ đó so sánh a với b.
