Trong không gian với hệ trục tọa độ $O x y z$, cho hai đường thẳng ${\ell _1}:x - 1 = \dfrac{{y + 2}}{2} =  - z$ và ${\ell _2}:\dfrac{{x - 3}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{{z - 1}}{2}$. Gọi $(Q)$ là mặt phẳng chứa ${\ell _1}$ và tạo với ${\ell _2}$ một góc lớn nhất là $\alpha$. Khi đó $\cos \alpha$ bằng

Bước 1: Giả sử phương trình của $(Q)$ có dạng $A(x - 1) + B(y + 2) + Cz = 0$. Gọi $\theta$ là góc giữa $(Q)$ và ${\ell _2}$. Biểu diễn $\sin \theta$ theo A, B.

Đường thẳng ${\ell _1}$ có một vectơ chỉ phương là ${\vec u_1} = (1;2; - 1)$ và đi qua điểm ${M_1} = (1; - 2;0).$ Vì $(Q)$ chứa ${\ell _1}$ nên đi qua ${M_1}$ và vectơ pháp tuyến của nó vuông góc với ${\vec u_1}.$ Do đó, ta có thể giả sử phương trình của $(Q)$ có dạng

$A(x - 1) + B(y + 2) + Cz = 0$ với $1 \cdot A + 2 \cdot B + ( - 1) \cdot C = 0$ và ${A^2} + {B^2} + {C^2} > 0$

Gọi $\theta$ là góc giữa $(Q)$ và ${\ell _2}$.

Do vectơ pháp tuyến của $(Q)$ là $\vec n = (A;B;C) =$ $(A;B;A + 2B)$ (vì $A + 2B = C$) và vectơ chỉ phương của ${\ell _2}$ là ${\vec u_2} = (2; - 1;2)$ nên ta có:

$\sin \theta  = \dfrac{{|4A + 3B|}}{{3\sqrt {2{A^2} + 4AB + 5{B^2}} }}$$= \dfrac{1}{3}\sqrt {\dfrac{{{{(4A + 3B)}^2}}}{{2{A^2} + 4AB + 5{B^2}}}}$

Bước 2: Ta xét hai trường hợp của B để tìm $\sin \theta$ rồi so sánh.

Ta xét hai trường hợp.

+) Trường hợp $B = 0$, thì $\sin \theta  = \dfrac{{2\sqrt 2 }}{3}$.

+) Trường hợp $B \ne 0$, ta đặt $r = \dfrac{A}{B}$ thì được $\sin \theta  = \dfrac{1}{3}\sqrt {\dfrac{{{{(4r + 3)}^2}}}{{2{r^2} + 4r + 5}}}$.

Từ đó, ta xét hàm số $f(r) = \dfrac{{{{(4r + 3)}^2}}}{{2{r^2} + 4r + 5}}$ trên $\mathbb{R}$.

${f^\prime }(r)$$= \dfrac{{8(4r + 3)\left( {2{r^2} + 4r + 5} \right) - {{(4r + 3)}^2}(4r + 4)}}{{{{\left( {2{r^2} + 4r + 5} \right)}^2}}}$$= \dfrac{{4(4r + 3)(r + 7)}}{{{{\left( {2{r^2} + 4r + 5} \right)}^2}}}$

Mặt khác $\mathop {\lim }\limits_{r \to  \pm \infty } f(r) = 8$ và $f\left( { - \dfrac{3}{4}} \right) = 0,f( - 7) = \dfrac{{25}}{3}$ nên ta lập được bảng biến thiên.

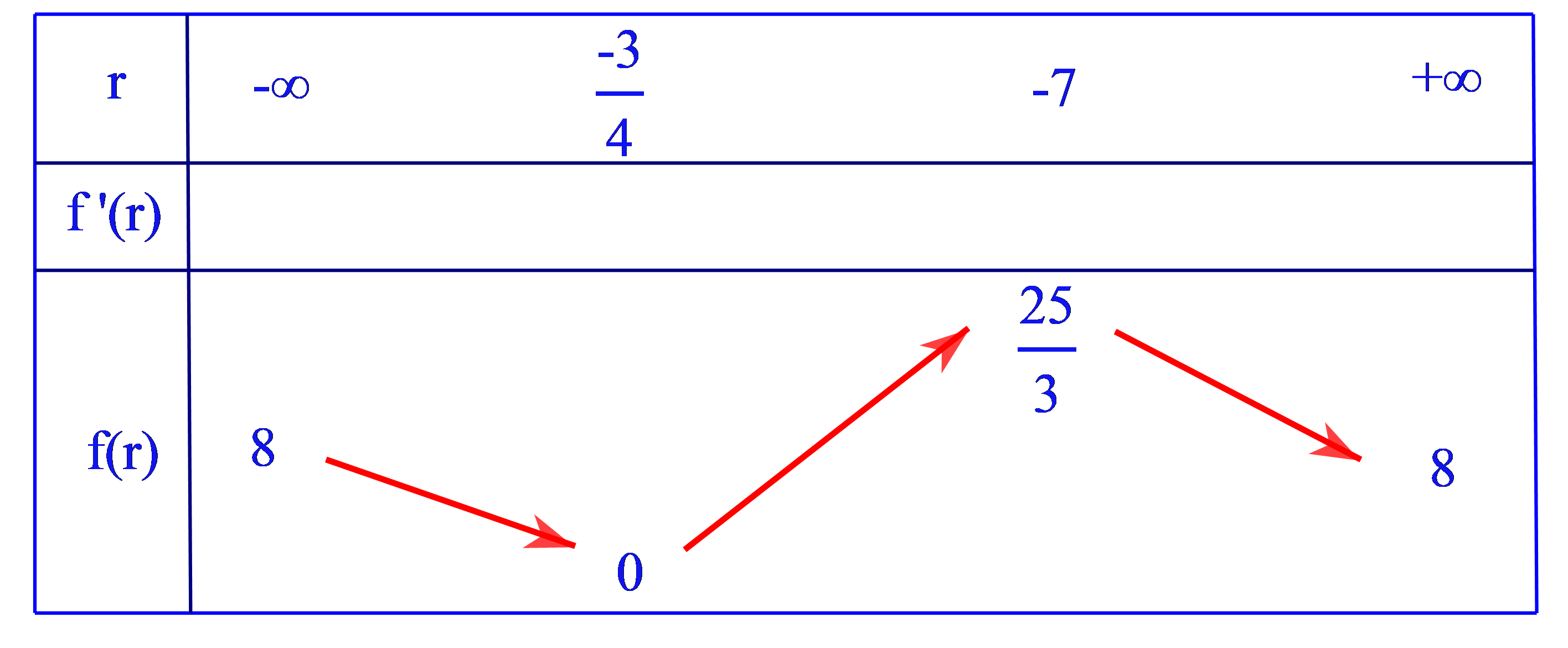
Từ đó thu được giá trị lớn nhất là $\dfrac{{25}}{3}$. Khi đó, $\sin \theta  = \dfrac{{5\sqrt 3 }}{9}$.

So sánh hai trường hợp trên, ta thu được $\sin \alpha  = \dfrac{{5\sqrt 3 }}{9}$. Từ đó $\cos \alpha  = \dfrac{{\sqrt 6 }}{9}$.