Câu hỏi:
2 năm trước
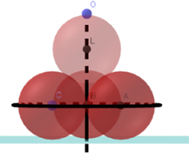
Có 4 viên bi hình cầu bán kính bằng 1cm. Người ta đặt 3 viên bi tiếp xúc nhau và cùng tiếp xúc với mặt bàn. Sau đó đai 3 viên bi đó lại và đặt 1 viên bi thứ 4 tiếp xúc vởi cả 3 viên bi trên như hình vẽ bên dưới. Gọi O là điểm thuộc bề mặt của viên bi thứ 4 có khoảng cách đến mặt bàn là lớn nhất. Khoảng cách từ O đến mặt bàn bằng
Trả lời bởi giáo viên
Đáp án đúng: b
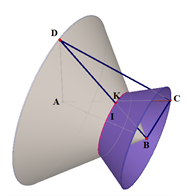
Tứ diện đều $ABCD$ có cạnh đều bằng $2$ (do $BC = BM + MC = 1 + 1 = 2$).
Tam giác $ACD$ đều, cạnh bằng $2$ => Chiều cao $AN = 2.\dfrac{{\sqrt 3 }}{2} = \sqrt 3 $
Tam giác $BCD $ đều, cạnh bằng $2$, $I$ là trọng tâm
=> $IN = \dfrac{1}{3}BN = \dfrac{1}{3}.\sqrt 3 = \dfrac{{\sqrt 3 }}{3}$
Tam giác $AIN$ vuông tại $I,$ theo Pytago ta có: $AI = \sqrt {A{N^2} - I{N^2}} = \sqrt {{{\left( {\sqrt 3 } \right)}^2} - {{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2}} = \sqrt {\dfrac{8}{3}} = \dfrac{{\sqrt {24} }}{3} = \dfrac{{2\sqrt 6 }}{3}$
Vậy, khoảng cách từ $O $ đến mặt bàn bằng $OJ = OA + AI + IJ = 1 + $ $\dfrac{{2\sqrt 6 }}{3}$ $+ 1 = $ $\dfrac{{6 + 2\sqrt 6 }}{3}$
Hướng dẫn giải:
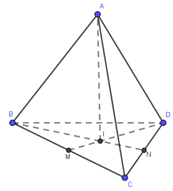
Gọi tâm của các viên bi lần lượt là $A, B, C, D.$
Vì 4 viên bi tiếp xúc nhau, nên các điểm tiếp xúc của đôi một 4 viên bi này là trung điểm của các cạnh của tứ diện đều $ABCD$.
Khoảng cách từ $O $ đến mặt bàn bằng $OJ = OA + AI + IJ$ ($I$ là tâm của tam giác $BCD$)
Tính $ AI.$
