Câu hỏi:
2 năm trước
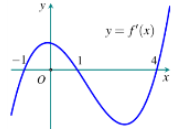
Cho hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ dưới đây:
Tìm số điểm cực trị của hàm số \(y = {e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\)
Trả lời bởi giáo viên
Đáp án đúng: d
Bước 1: Tính y'
Ta có:
\(\begin{array}{l}y = {e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\\y' = 2f'\left( x \right).{e^{2f\left( x \right) + 1}} + f'\left( x \right){.5^{f\left( x \right)}}.\ln 5\\ = f'\left( x \right)\left[ {2{e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\ln 5} \right]\end{array}\)
Bước 2: Chứng minh dấu của y' chỉ phụ thuộc vào dấu của $f'(x)$ và tìm số cực trị.
Ta thấy \(2{e^{2f\left( x \right) + 1}} + {5^{f\left( x \right)}}\ln 5 > 0\forall x\)
=> Dấu của y’ phụ thuộc vào dấu của \(f'\left( x \right)\).
Dựa vào đồ thị ta thấy \(f'\left( x \right)\) đổi dấu 3 lần nên số điểm cực trị của hàm số ban đầu là 3.
Hướng dẫn giải:
Bước 1: Tính y'
Bước 2: Chứng minh dấu của y' chỉ phụ thuộc vào dấu của $f'(x)$ và tìm số cực trị.
