Câu hỏi:
2 năm trước
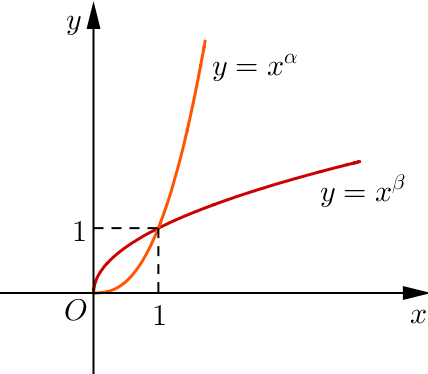
Cho \(\alpha ,\beta \) là các số thực. Đồ thị các hàm số \(y = {x^\alpha },y = {x^\beta }\), trên khoảng \(\left( {0; + \infty } \right)\) được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
Với \({x_0} > 1\) ta có:
\(x_0^\alpha > 1 \Rightarrow \alpha > 0;x_0^\beta > 1 \Rightarrow \beta > 0\).
\(x_0^\alpha > x_0^\beta \Rightarrow \alpha > \beta \)
Mặt khác, dựa vào hình dáng đồ thị ta suy ra \(\alpha > 1\) và \(\beta < 1\)
Từ đó suy ra A là phương án đúng.
Hướng dẫn giải:
Lấy \({x_0} > 1\), so sánh các giá trị \(x_0^\alpha ,x_0^\beta \) rồi suy ra \(\alpha ,\beta \)