Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f'\left( x \right)\) cho như hình dưới đây. Đặt \(g\left( x \right) = 2f\left( x \right) - {\left( {x + 1} \right)^2}\). Mệnh đề nào dưới đây đúng.
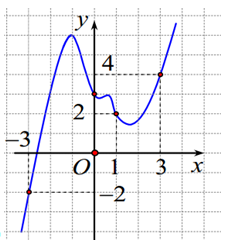
Trả lời bởi giáo viên
Ta có \(g\left( x \right) = 2f\left( x \right) - {\left( {x + 1} \right)^2}\)
\( \Rightarrow g'\left( x \right) = 2f'\left( x \right) - \left( {2x + 2} \right) = 0 \Leftrightarrow f'\left( x \right) = x + 1\).
Quan sát trên đồ thị ta có hoành độ giao điểm của \(f'\left( x \right)\) và \(y = x + 1\) trên khoảng \(\left( { - 3;3} \right)\) là \(x = 1\).
Vậy ta so sánh các giá trị \(g\left( { - 3} \right)\), \(g\left( 1 \right)\), \(g\left( 3 \right)\)
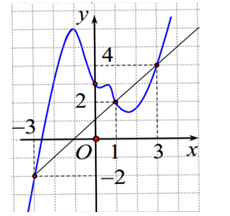
Xét \(\int\limits_{ - 3}^1 {g'\left( x \right)} {\rm{d}}x = 2\int\limits_{ - 3}^1 {\left[ {f'\left( x \right) - \left( {x + 1} \right)} \right]} {\rm{d}}x > 0\)
\( \Leftrightarrow g\left( 1 \right) - g\left( { - 3} \right) > 0 \Leftrightarrow g\left( 1 \right) > g\left( { - 3} \right)\)
Tương tự xét \(\int\limits_1^3 {g'\left( x \right)} {\rm{d}}x = 2\int\limits_1^3 {\left[ {f'\left( x \right) - \left( {x + 1} \right)} \right]} {\rm{d}}x < 0\)\( \Leftrightarrow g\left( 3 \right) - g\left( 1 \right) < 0 \Leftrightarrow g\left( 3 \right) < g\left( 1 \right)\)
Xét \(\int\limits_{ - 3}^3 {g'\left( x \right)} {\rm{d}}x = 2\int\limits_{ - 3}^1 {\left[ {f'\left( x \right) - \left( {x + 1} \right)} \right]} {\rm{d}}x + 2\int\limits_1^3 {\left[ {f'\left( x \right) - \left( {x + 1} \right)} \right]} {\rm{d}}x > 0\)
\( \Leftrightarrow g\left( 3 \right) - g\left( { - 3} \right) > 0 \Leftrightarrow g\left( 3 \right) > g\left( { - 3} \right)\).
Suy ra ta có \(g\left( 1 \right) > g\left( 3 \right) > g\left( { - 3} \right)\).
Vậy \(\mathop {\max }\limits_{\left[ { - 3;3} \right]} g\left( x \right) = g\left( 1 \right)\).
Hướng dẫn giải:
- Tính \(g'\left( x \right)\) và giải phương trình \(g'\left( x \right) = 0\)
- Tìm \(GTLN,GTNN\) của \(g\left( x \right)\) trên đoạn \(\left[ { - 3;3} \right]\)

