Cho phương trình \({2^x} + m = \log {_2}\left( {x - m} \right)\) với \(m\) là tham số. Có bao nhiêu giá trị nguyên của \(m \in \left( { - 18;\;18} \right)\) để phương trình đã cho có nghiệm?

Điều kiện: \(x - m > 0 \Leftrightarrow x > m.\)

Đặt: \({2^x} + m = {\log _2}\left( {x - m} \right) = y \Rightarrow \left\{ \begin{array}{l}{2^x} + m = y\\{\log _2}\left( {x - m} \right) = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{2^x} + m = y\\x - m = {2^y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{2^x} + x = {2^y} + y\;\;\;\;\;\left( * \right)\\m = x - {2^y}\;\;\;\;\;\;\;\;\;\;\;\left( {**} \right)\end{array} \right..\)

Xét hàm số đặc trưng: \(f\left( t \right) = {2^t} + t\) ta có: \(f'\left( t \right) = {2^t}\ln 2 + 1 > 0,\forall t.\)

\( \Rightarrow f\left( t \right)\) đồng biến trên \(R.\)

Khi đó ta có: \(\left( * \right) \Leftrightarrow f\left( x \right) = f\left( y \right) \Leftrightarrow x = y.\)

\( \Rightarrow \left( {**} \right) \Leftrightarrow m = x - {2^x}\;\;\;\;\left( {***} \right).\)

Xét hàm số: \(g\left( x \right) = x - {2^x}\) có: $g'\left( x \right) = 1 - {2^x}\ln 2.$

\( \Rightarrow g'\left( x \right) = 0 \Leftrightarrow 1 - {2^x}\ln 2 = 0 \Leftrightarrow {2^x} = \dfrac{1}{{\ln 2}}\) \( \Leftrightarrow x = {\log _2}\left( {\dfrac{1}{{\ln 2}}} \right) =  - {\log _2}\left( {\ln 2} \right).\)

Ta có BBT:

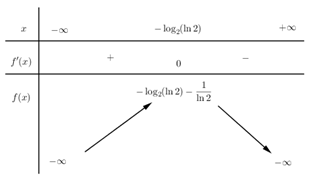
\( \Rightarrow \;\left( {***} \right)\) có nghiệm $ \Leftrightarrow m \le  - \log { _2}\left( {\ln 2} \right) - \dfrac{1}{{\ln 2}} \approx  - 0,914$

Với \(m \in \left( { - 18;\;18} \right)\) và \(m \in Z \Rightarrow m \in \left\{ { - 17; - 16;....; - 2; - 1} \right\}.\)

Vậy có $17$ giá trị \(m\) thỏa mãn.