Xét các số thực dương $x,{\rm{ }}y$ thỏa mãn \({\log _{\dfrac{1}{3}}}x + {\log _{\dfrac{1}{3}}}y \le {\log _{\dfrac{1}{3}}}\left( {{x^2} + y} \right)\). Tìm giá trị nhỏ nhất ${P_{\min }}$ của biểu thức $P{\rm{ }} = {\rm{ }}3x{\rm{ }} + {\rm{ }}2y.$

\({\log _{\dfrac{1}{3}}}x + {\log _{\dfrac{1}{3}}}y \le {\log _{\dfrac{1}{3}}}\left( {{x^2} + y} \right) \Leftrightarrow {\log _{\dfrac{1}{3}}}\left( {xy} \right) \le {\log _{\dfrac{1}{3}}}\left( {{x^2} + y} \right) \Leftrightarrow xy \ge {x^2} + y \Leftrightarrow y\left( {x - 1} \right) \ge {x^2}\)

Với x = 1 ta có \(0 \ge 1\) (Vô lý) \( \Rightarrow x \ne 1\) .

Ta có \(y\left( {x - 1} \right) = {x^2} \ge 0,\)  mà \(y > 0 \Rightarrow x - 1 \ge 0 \Leftrightarrow x \ge 1.\)  Vậy \(x > 1\)

Khi đó ta có :

\(P = 3x + 2y = \dfrac{{\left( {3x + 2y} \right)\left( {x - 1} \right)}}{{x - 1}} = \dfrac{{3x\left( {x - 1} \right) + 2y\left( {x - 1} \right)}}{{x - 1}} \ge \dfrac{{3{x^2} - 3x + 2{x^2}}}{{x - 1}} = \dfrac{{5{x^2} - 3x}}{{x - 1}} = f\left( x \right)\,\,\,\forall x > 1\)

Xét hàm số \(f\left( x \right) = \dfrac{{5{x^2} - 3x}}{{x - 1}} = 5x + 2 + \dfrac{2}{{x - 1}}\,\,\,\left( {x > 1} \right)\) ta có

$f'\left( x \right) = 5 - \dfrac{2}{{{{\left( {x - 1} \right)}^2}}} = \dfrac{{5{{\left( {x - 1} \right)}^2} - 2}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 + \dfrac{{\sqrt {10} }}{5}\\x = 1 - \dfrac{{\sqrt {10} }}{5}\end{array} \right.$

BBT :

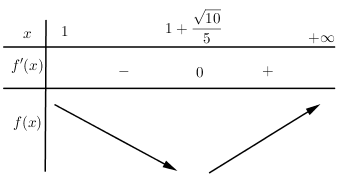
Dựa vào BBT ta thấy

\(\begin{array}{l}\mathop {\min }\limits_{\left( {1; + \infty } \right)} f\left( x \right) = f\left( {1 + \dfrac{{\sqrt {10} }}{5}} \right) = 5\left( {1 + \dfrac{{\sqrt {10} }}{5}} \right) + 2 + \dfrac{2}{{1 + \dfrac{{\sqrt {10} }}{5} - 1}} = 5 + \sqrt {10}  + 2 + \sqrt {10}  = 7 + 2\sqrt {10} \\ \Rightarrow P \ge f\left( x \right) \ge 7 + 2\sqrt {10}  \Rightarrow {P_{\min }} = 7 + 2\sqrt {10} \end{array}\)