Câu hỏi:
2 năm trước
Cho hệ $\left\{ \begin{array}{l}9{x^2} - 4{y^2} = 5\\{\log _m}(3x + 2y) - {\log _3}(3x - 2y) = 1\end{array} \right.$ có nghiệm $\left( {x;y} \right)$ thỏa mãn $3x + 2y \le 5$. Khi đó giá trị lớn nhất của $m$ là:
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có: $9{x^2} - 4{y^2} = 5 \Leftrightarrow (3x - 2y)(3x + 2y) = 5$$ \Leftrightarrow 3x - 2y = \dfrac{5}{{3x + 2y}}$
Khi đó, ta có:
$\begin{array}{l}{\log _m}(3x + 2y) - {\log _3}(3x - 2y) = 1 \Leftrightarrow {\log _m}(3x + 2y) - {\log _3}\dfrac{5}{{3x + 2y}} = 1\\ \Leftrightarrow \dfrac{{{{\log }_3}(3x + 2y)}}{{{{\log }_3}m}} - {\log _3}5 + {\log _3}(3x + 2y) = 1\\ \Leftrightarrow \dfrac{{{{\log }_3}(3x + 2y)}}{{{{\log }_3}m}} = {\log _3}5 - {\log _3}(3x + 2y) + 1\\ \Leftrightarrow {\log _3}m = \dfrac{{{{\log }_3}(3x + 2y)}}{{{{\log }_3}5 - {{\log }_3}(3x + 2y) + 1}}\,\,(1)\end{array}$
Đặt \(t = {\log _3}\left( {3x + 2y} \right) \le {\log _3}5\) thì \(\left( 1 \right)\) trở thành \({\log _3}m = \dfrac{t}{{{{\log }_3}5 - t + 1}}\)
Xét hàm số $y = f(t) = \dfrac{t}{{{{\log }_3}5 - t + 1}},t \in \left( { - \infty ;{{\log }_3}5} \right]$
$f'(t) = \dfrac{{{{\log }_3}5 + 1}}{{{{({{\log }_3}5 - t + 1)}^2}}} > 0,\,\,\forall t \in \left( { - \infty ;{{\log }_3}5} \right]$
Bảng biến thiên:
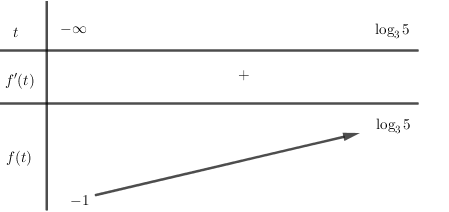
Để $\left( 1 \right)$ có nghiệm thì $ - 1 < \log { _3}m \le {\log _3}5\, \Rightarrow \dfrac{1}{3} < m \le 5$
Vậy giá trị lớn nhất của $m$ thỏa mãn yêu cầu đề bài là $5.$
Hướng dẫn giải:
- Rút \(3x - 2y\) từ phương trình trên thay vào phương trình dưới
- Đặt ẩn phụ \(t = {\log _3}\left( {3x + 2y} \right)\) ở phương trình mới có được, tìm điều kiện của \(t\)
- Cô lập \(m\) và xét hàm \(f\left( t \right)\) trong khoảng \(t\) vừa tìm được ở trên, từ đó suy ra điều kiện cần tìm của \(m\)
