Cho số phức \(z\) thỏa mãn \(\left| {2z - 3 - 4i} \right| = 10.\) Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(\left| z \right|.\) Khi đó \(M - m\) bằng:
Trả lời bởi giáo viên
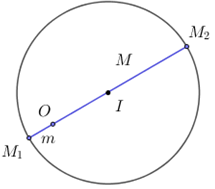
Giả sử điểm \(M\left( {x;\;y} \right)\) biểu diễn số phức \(z \Rightarrow z = x + yi \Rightarrow \left| z \right| = \sqrt {{x^2} + {y^2}} .\)
|
|
Ta có: \(\left| {2z - 3 - 4i} \right| = 10 \Leftrightarrow \left| {z - \dfrac{3}{2} - 2i} \right| = 5 \Leftrightarrow {\left( {x - \dfrac{3}{2}} \right)^2} + {\left( {y - 2} \right)^2} = 25.\)
\( \Rightarrow M\) thuộc đường tròn tâm \(I\left( {\dfrac{3}{2};\;2} \right)\) và bán kính \(R = 5.\)
\( \Rightarrow \left| z \right| = \sqrt {{x^2} + {y^2}} = OM.\) Ta đưa bài toán về tìm min và max của \(OM.\)
Ta có: \(OI = \sqrt {{{\left( {\dfrac{3}{2}} \right)}^2} + {2^2}} = \dfrac{5}{2} < R \Rightarrow I\) nằm trong đường tròn.
\( \Rightarrow OM\) đạt Max và Min khi \(M \in \) đường thẳng đi qua \(O,\;I.\)
\(\begin{array}{l} \Rightarrow M = Max\;OM = R + OI = 5 + \dfrac{5}{2} = \dfrac{{15}}{2}\\m = Min\;\;OM = R - OI = 5 - \dfrac{5}{2} = \dfrac{5}{2}.\\ \Rightarrow M - m = \dfrac{{15}}{2} - \dfrac{5}{2} = 5.\end{array}\)
Hướng dẫn giải:
+) Modun của số phức \(z = a + bi\) là \(\left| z \right| = \sqrt {{a^2} + {b^2}} .\)

