Câu hỏi:
3 năm trước
Gọi \(\varphi \) là 1 acgumen của số phức \(z\) có điểm biểu diễn là \(M\left( {\dfrac{1}{2};\dfrac{{\sqrt 3 }}{2}} \right)\) nằm trên đường tròn đơn vị, số đo nào sau đây có thể là một acgumen của \(z\)?
Trả lời bởi giáo viên
Đáp án đúng: b
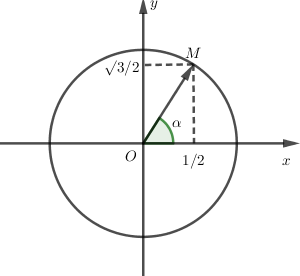
Quan sát hình vẽ ta thấy \(\left\{ \begin{array}{l}\sin \varphi = \dfrac{{\sqrt 3 }}{2}\\\cos \varphi = \dfrac{1}{2}\end{array} \right. \Rightarrow \varphi = \dfrac{\pi }{3}\)
Hướng dẫn giải:
Biểu diễn \(M\) trên đường tròn đơn vị và tìm góc \(\varphi = \widehat {\left( {Ox,OM} \right)}\)

