Trả lời bởi giáo viên
Đáp án đúng: d
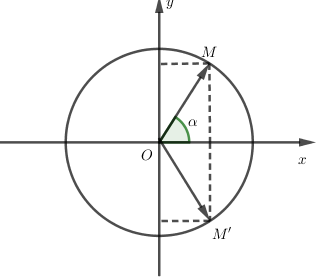
Số phức z có điểm biểu diễn là M thì ¯z có điểm biểu diễn là M′ đối xứng với M qua Ox. Do đó −φ là một argument của ¯z.
Số phức z=a+bi được viết dưới dạng lượng giác là z=r.(cosφ+isinφ)
Với r=|z| và φ là argument của z.
Khi đó
¯z=r.(cosφ−i.sinφ)=r.[cos(−φ)+i.sin(−φ)]

