Chọn mệnh đề đúng:
Phép vị tự tỉ số \(k \ne \pm 1\) làm thay đổi độ dài đoạn thẳng nên nó không phải phép dời hình nên A sai.
Phép vị tự tỉ số $k=-1$ là phép đối xứng tâm nên nó là phép dời hình, B sai.
Không có phép vị tự tỉ số \(k = 0\) nên D sai.
Phép vị tự tỉ số \(k = 1\) là phép đồng nhất nên nó là phép dời hình.
Nếu tỉ số vị tự \(k = - 1\) thì phép vị tự là:
Phép vị tự tỉ số \(k = - 1\) là phép đối xứng tâm.
Chọn mệnh đề đúng:
Hai hình đồng dạng thì chưa chắc bằng nhau nên A sai.
Hai hình bằng nhau thì đồng dạng nên B đúng, D sai.
Hai hình đồng dạng sẽ trùng nhau nếu phép đồng dạng là phép đồng nhất nên C sai.
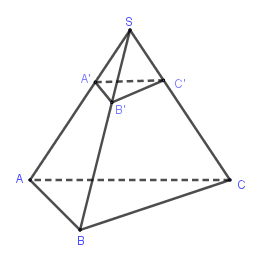
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là:
Ta có: \(A'A = 2SA',B'B = 2SB',C'C = 2SC' \)
$\Rightarrow \overrightarrow {SA'} = \dfrac{1}{3}\overrightarrow {SA} ,\overrightarrow {SB'} = \dfrac{1}{3}\overrightarrow {SB} ,\overrightarrow {SC'} = \dfrac{1}{3}\overrightarrow {SC} $
Do đó phép vị tự tâm \(S\) tỉ số \(k = \dfrac{1}{3}\) biến các điểm \(A,B,C\) thành \(A',B',C'\).
Trong các mệnh đề sau, mệnh đề nào sai?
Các hình tứ diện đều, lập phương, bát diện đều là các khối đa diện đều nên chúng là đa diện lồi.
Hình tạo bởi hai tứ diện đều ghép với nhau có thể là đa diện lồi hoặc không phải là đa diện lồi
⇒ Mệnh đề “Hình tạo bởi hai tứ diện đều ghép với nhau là đa diện lồi” là mệnh đề sai
Khối mười hai mặt đều là khối đa diện đều loại:
Khối mười hai mặt đều thuộc loại \(\left\{ {5;3} \right\}\).
Có tất cả bao nhiêu loại khối đa diện đều?
Chỉ có $5$ loại khối đa diện đều là tứ diện đều, khối lập phương, khối bát diện đều, khối $12$ mặt đều và khối $20$ mặt đều.
Khối đa diện đều loại \(\left\{ {n;p} \right\}\) thì \(n\) là:
- Khối đa diện đều loại \(\left\{ {n;p} \right\}\):
+ \(n\) là số cạnh của mỗi mặt.
+ \(p\) là số cạnh cùng đi qua một đỉnh.
Vì số đỉnh mỗi mặt bằng số cạnh mỗi mặt nên \(n\) cũng số đỉnh mỗi mặt.
Trong các kí hiệu sau, kí hiệu nào không phải của khối đa diện đều?
Có \(5\) khối đa diện, đó các loại \(\left\{ {3;3} \right\},\left\{ {4;3} \right\},\left\{ {3;4} \right\},\left\{ {5;3} \right\},\left\{ {3;5} \right\}\)
Vậy kí hiệu \(\left\{ {4;4} \right\}\) không phải kí hiệu của khối đa diện đều nào cả.
Khối đa diện đều có $20$ mặt thì có bao nhiêu cạnh?
Khối đa diện $20$ mặt đều thuộc loại \(\left\{ {3;5} \right\}\) nên mỗi mặt có $3$ cạnh
Mỗi cạnh là cạnh chung của $2$ mặt nên tổng số cạnh của đa diện là $20.3:2 = 30$ (cạnh)
Hình vẽ sau đây là hình trải phẳng của khối đa diện đều nào?
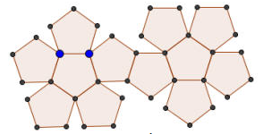
Quan sát hình vẽ ta thấy nó có \(12\) mặt và mỗi mặt là một ngũ giác đều.
Vậy hình vẽ trên là hình trải phẳng của khối mười hai mặt đều.
Mệnh đề nào sau đây là mệnh đề đúng?
Đa diện đều có tất cả các mặt là các đa giác bằng nhau.
Không tồn tại đa diện đều có $5$ và $6$ đỉnh, do đó chóp $S.ABCD$ và lăng trụ $ABC.A'B'C'$ không thể là đa diện đều.
Nếu mỗi đỉnh là đỉnh chung của đúng $3$ mặt thì nó cũng là đỉnh chung của đúng $3$ cạnh. Giả sử số đỉnh của đa diện là $n$ thì số cạnh của nó phải là $\dfrac{{3n}}{2}$ (vì mỗi cạnh được tính $2$ lần), do đó $n$ chẵn.
Khối đa diện đều nào sau đây có các mặt không phải là tam giác đều
Bát diện đều có $8$ mặt là các tam giác đều.
Nhị thập diện đều có $20$ mặt là các tam giác đều.
Tứ diện đều có $4$ mặt là các tam giác đều.
Thập nhị diện đều có $12$ mặt là các ngũ giác đều.
Hình đa diện đều có tất cả các mặt là ngũ giác có bao nhiêu cạnh?
Hình đa diện đều có tất cả các mặt là ngũ giác là khối mười hai mặt đều thuộc loại \(\left\{ {5;3} \right\}\) và có $30$ cạnh
Cho khối đa diện lồi có số đỉnh, số mặt và số cạnh lần lượt là \(D,M,C\). Chọn mệnh đề đúng:
Khối đa diện lồi có \(D\) đỉnh, \(M\) mặt và \(N\) cạnh thì \(D - C + M = 2\).
Cho khối đa diện lồi có \(8\) mặt và \(6\) đỉnh. Số cạnh của nó là:
Ta có: \(D = 6,M = 8\) thì \(D - C + M = 2 \Leftrightarrow 6 - C + 8 = 2 \Leftrightarrow C = 12\)
Vậy số cạnh là \(12\).
Có bao nhiêu cách chọn ra ba đỉnh từ các đỉnh của một hình lập phương để thu được một tam giác đều ?
Nối các đường chéo của các mặt ta được 2 tứ diện đều không có đỉnh nào chung.
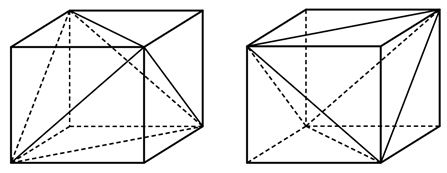
Mỗi tứ diện đều có 4 tmặt là 4 tam giác đều. Nên tổng cộng có 8 tam giác đều.
Cho hình đa diện đều loại \(\left\{ {4;3} \right\}\) có cạnh bằng a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?
Khối đa diện đều loại \(\left\{ {4;3} \right\}\) là hình lập phương. Khối lập phương có 6 mặt là hình vuông cạnh a.
Diện tích một mặt là \({a^2}\).
Vậy tổng diện tích các mặt của hình lập phương đó là: \(S = 6{a^2}\).
Khối đa diện đều loại \(\left\{ {3;4} \right\}\)có tất cả bao nhiêu cạnh?
Khối đa diện đều loại \(\left\{ {3;4} \right\}\) là bát diện đều. Khối bát diện đều có 12 cạnh.
Số đỉnh của hình 12 mặt đều là:
Hình 12 mặt đều có số đỉnh là hai mươi.

