Cho hình hộp đứng $ABCD.A’B’C’D’$ có đáy $ABCD$ là hình thoi cạnh $a$ và $\widehat {BAD} = {60^0}$, $AB’$ hợp với đáy $(ABCD)$ một góc ${30^0}$. Thể tích của khối hộp là
Trả lời bởi giáo viên
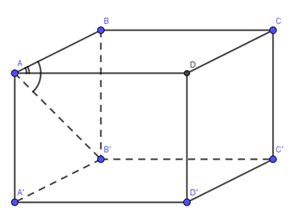
$ABCD.A’B’C’D’$ là hình hộp đứng
$ \Rightarrow BB' \bot (ABCD) \Rightarrow \left( {\widehat {AB',(ABCD)}} \right) = \left( {\widehat {AB';AB}} \right) = \widehat {BAB'} = {30^0}$
Tam giác $ABB’$ vuông tại $B$ $ \Rightarrow \tan \widehat {BAB'} = \dfrac{{BB'}}{{AB}}$
$ \Rightarrow BB' = AB.\tan {30^0} = \dfrac{a}{{\sqrt 3 }}$
Tam giác $ABD $ có: $AB = AD = a,$ $\widehat {BAD} = {60^0} \Rightarrow $ Tam giác $ABD$ đều, có cạnh đều bằng $a.$
$ \Rightarrow {S_{ABD}} = \dfrac{{{a^2}\sqrt 3 }}{4} \Rightarrow {S_{ABCD}} = 2\,{S_{ABD}} = 2.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}$
Thể tích khối hộp $ABCD.A’B’C’D’$: $V = {S_{ABCD}}.BB' = \dfrac{{{a^2}\sqrt 3 }}{2}.\dfrac{a}{{\sqrt 3 }} = \dfrac{{{a^3}}}{2}$.
Hướng dẫn giải:
Thể tích khối hộp : ${V_{hop}} = {S_{day}}.h$

