Cho khối chóp tứ giác $S.ABCD.$ Mặt phẳng đi qua trọng tâm các tam giác \(SAB,\;SAC,\;\;SAD\) chia khối chóp này thành hai phần có thể tích là \({V_1}\) và \({V_2}\;\;\left( {{V_1} < {V_2}} \right).\) Tính tỉ lệ \(\dfrac{{{V_1}}}{{{V_2}}}.\)

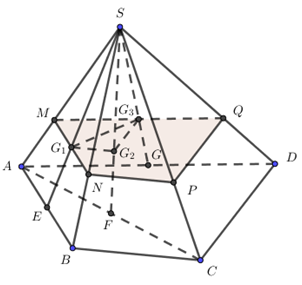
Gọi \({G_1};{G_2};{G_3}\) lần lượt là trực tâm các tam giác SAB, SAC và SAD.

Gọi E, F, G lần lượt là trung điểm của AB, AC và AD ta có:

\(\dfrac{{S{G_1}}}{{SE}} = \dfrac{{S{G_2}}}{{SF}} = \dfrac{{S{G_3}}}{{SG}} = \dfrac{2}{3} \Rightarrow {G_1}{G_2}//EF;\,\,{G_2}{G_3}//FG \Rightarrow \left( {{G_1}{G_2}{G_3}} \right)//\left( {EFG} \right)\)

Hay \(\left( {{G_1}{G_2}{G_3}} \right)//\left( {ABC} \right)\)

Qua \({G_1}\) kẻ MN // AB \(\left( {M \in SA;N \in SB} \right)\).

Qua \({G_3}\) kẻ \(MQ//AD\,\,\left( {Q \in SD} \right)\)

Qua N kẻ \(NP//BC\,\,\left( {N \in SC} \right)\)

\( \Rightarrow \) Thiết diện của khối chóp cắt bởi mặt phẳng \(\left( {{G_1}{G_2}{G_3}} \right)\) là \(\left( {MNPQ} \right)\), chia khối chóp thành hai phần : \(S.MNPQ\) và \(MNPQ.ABCD\).

Áp dụng định lí Ta-lét ta tính được \(\dfrac{{SM}}{{SA}} = \dfrac{{SN}}{{SB}} = \dfrac{{SP}}{{SC}} = \dfrac{{SQ}}{{SD}} = \dfrac{2}{3}\).

Ta có \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}} = \dfrac{2}{3}.\dfrac{2}{3}.\dfrac{2}{3} = \dfrac{8}{{27}} \Rightarrow {V_{S.MNP}} = \dfrac{8}{{27}}{V_{S.ABC}}\)

         \(\dfrac{{{V_{S.MPQ}}}}{{{V_{S.ACD}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SP}}{{SC}}.\dfrac{{SQ}}{{SD}} = \dfrac{2}{3}.\dfrac{2}{3}.\dfrac{2}{3} = \dfrac{8}{{27}} \Rightarrow {V_{S.MPQ}} = \dfrac{8}{{27}}{V_{S.ACD}}\)

\(\begin{array}{l} \Rightarrow {V_{S.MNPQ}} = {V_{S.MNP}} + {V_{S.MPQ}} = \dfrac{8}{{27}}\left( {{V_{S.ABC}} + {V_{S.ACD}}} \right) = \dfrac{8}{{27}}{V_{S.ABCD}}\\ \Rightarrow {V_1} = \dfrac{8}{{27}}{V_{S.ABCD}};\,\,{V_2} = \dfrac{{19}}{{27}}{V_{S.ABCD}}\\ \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{8}{{19}}\end{array}\)