Cho hình chóp tứ giác đều $S.ABCD,$ đường cao $SO.$ Biết rằng trong các thiết diện của hình chóp cắt bởi các mặt phẳng chứa $SO,$ thiết diện có diện tích lớn nhất là tam giác đều cạnh bằng $a,$ tính thể tích khối chóp đã cho.
Trả lời bởi giáo viên
Gọi $\left( \alpha \right)$ là mặt phẳng chứa $SO,$ cắt mặt đáy \(\left( {ABCD} \right)\) theo giao tuyến là đường thẳng \(MN\) với \(M,N\) thuộc các cạnh của hình vuông \(ABCD\).
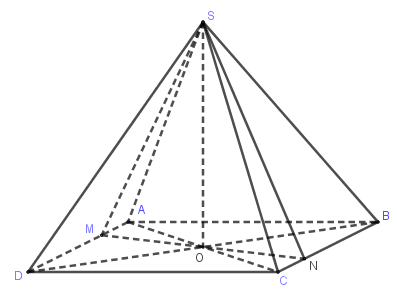
Không mất tính tổng quát ta giả sử \(MN\) như hình vẽ.
Ta có : \({S_{SMN}} = \dfrac{1}{2}SO.MN \le \dfrac{1}{2}SO.AC = {S_{SAC}} = const\)
Do đó \({S_{SMN}}\) đạt giá trị lớn nhất bằng \({S_{SAC}}\) khi \(MN = AC=BD\).
Mà tam giác $SMN $ đều cạnh $a$ nên $AC=BD=a$
\(\Rightarrow {S_{ABCD}} = \dfrac{1}{2}AC.BD = \dfrac{{{a^2}}}{2}\) và \(SO = \dfrac{{a\sqrt 3 }}{2}\).
Thể tích \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)
Hướng dẫn giải:
Diện tích thiết diện lớn nhất đạt được khi giao tuyến của nó với đáy chính là đường chéo của hình vuông.

