Câu hỏi:
2 năm trước
Cho hình hộp $ABCD.A’B’C’D’$ có tất cả các cạnh bằng $a,$ hình chiếu vuông góc của $A’$ lên mặt phẳng $(ABCD)$ nằm trong tứ giác $ABCD,$ các cạnh xuất phát từ đỉnh $A$ của hình hộp tạo với nhau một góc $60^0.$ Tính thể tích khối hộp $ABCD.A’B’C’D’.$
Trả lời bởi giáo viên
Đáp án đúng: a
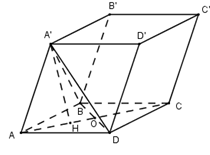
Gọi $H$ là chân đường vuông góc hạ từ đỉnh $A’$ lên $(ABCD).$
Vì $\widehat {A'AB} = \widehat {A'AD} = \widehat {BAD} = {60^0} \Rightarrow $ Các tam giác $AA’B, ABD$ và $AA’D$ là các tam giác đều cạnh $a$ \( \Rightarrow A'A = A'B' = A'D = a \)
\(\Rightarrow \) Hình chóp $A’.ABD$ có các cạnh bên bằng nhau nên $H$ là tâm của tam giác đều $ABD.$
Dễ dàng tính được \(AH = \dfrac{2}{3}AO = \dfrac{2}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Xét tam giác vuông $AA’H$ có \(A'H = \sqrt {A'{A^2} - A{H^2}} = \dfrac{{a\sqrt 6 }}{3}\)
\(\begin{array}{l}{S_{ABCD}} = 2{S_{ABD}} = 2\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}\\ \Rightarrow {V_{ABCD.A'B'C'D'}} = \dfrac{{a\sqrt 6 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 2 }}{2}\end{array}\)
Hướng dẫn giải:
+) Gọi $H$ là chân đường vuông góc hạ từ đỉnh $A’$ lên $(ABCD).$ Xác định chính xác vị trí của điểm $H$ trên $(ABCD).$
+) \({V_{ABCD.A'B'C'D'}} = A'H.{S_{ABCD}}\)
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
