Cho hình chóp \(S.ABC\) có \(AB = 3,BC = 4,AC = 5\). Tính thể tích khối chóp \(S.ABC\) biết rằng cắc mặt bên tạo với đáy một góc \({30^0}\) và hình chiếu vuông góc của \(S\) trên \(\left( {ABC} \right)\) nằm trong tam giác \(ABC\)
Trả lời bởi giáo viên
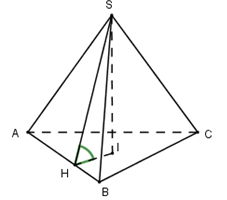
Gọi $I$ là tâm đường tròn nội tiếp \(\Delta ABC \Rightarrow SI \bot \left( {ABC} \right)\)
Dễ thấy \(\Delta ABC\) vuông tại \(B \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}BA.BC = \dfrac{1}{2}.3.4 = 6\), nửa chu vi \(\Delta ABC:\,\,p = \dfrac{{3 + 4 + 5}}{2} = 6\)
Gọi \(H\) là hình chiếu của \(I\) trên cạnh \(AB\) ta có
\(S = p.r \Rightarrow r = \dfrac{S}{p} = 1\), với $r$ là tâm đường tròn nội tiếp \(\Delta ABC \Rightarrow IH = 1\).
\(\left\{ \begin{array}{l}AB \bot IH\\AB \bot SI\end{array} \right. \Rightarrow AB \bot \left( {SHI} \right) \Rightarrow AB \bot SH \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SH;IH} \right)} = \widehat {SHI} = {30^0}\)
Xét tam giác vuông \(SHI\) có \(SI = HI.\tan 30 = \dfrac{1}{{\sqrt 3 }}\)
Vậy \({V_{S.ABC}} = \dfrac{1}{3}SI.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{1}{{\sqrt 3 }}.6 = \dfrac{{2\sqrt 3 }}{3}\)
Hướng dẫn giải:
Hình chóp có các mặt bên tạo với đáy góc bằng nhau có hình chiếu của đỉnh trùng với tâm đường tròn nội tiếp đáy.

