Cho hình hộp $ABCD.A'B'C'D'$. Gọi $E,F$ lần lượt là trung điểm của $B'C'$ và $C'D'$. Mặt phẳng $\left( {AEF} \right)$ chia hình hộp thành hai hình đa diện $\left( H \right)$ và $\left( {H'} \right)$ trong đó $\left( H \right)$ là hình đa diện chứa đỉnh $A'$. Tính tỉ số thể tích đa diện $\left( H \right)$ và thể tích hình đa diện $\left( {H'} \right)$.

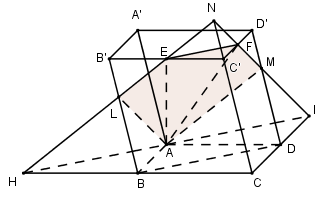
Mặt phẳng $\left( {AEF} \right)$ chứa $EF//BD \subset \left( {ABCD} \right)$

$\Rightarrow$ Giao tuyến của $\left( {AEF} \right)$ và $\left( {ABCD} \right)$ là đường thẳng đi qua $A$ và song song với $EF$

Trong $\left( {ABCD} \right)$ qua $A$ kẻ $HI//BD\,\,\left( {H \in BC,I \in CD} \right)$

Trong $\left( {BCC'B'} \right)$ gọi $L = EH \cap BB'$, trong $\left( {CDD'C'} \right)$ gọi $M = FI \cap DD'$, khi đó $\left( {AEF} \right) \equiv \left( {ALEFM} \right)$

Ta có : $\left\{ \begin{array}{l}\left( {AEF} \right) \cap \left( {BCC'B'} \right) = HE\\\left( {AEF} \right) \cap \left( {CDD'C'} \right) = FI\\\left( {BCC'B'} \right) \cap \left( {CDD'C'} \right) = CC'\end{array} \right.$

$\Rightarrow HE,FI,CC'$ đồng quy tại $N$.

Ta có : ${V_{H'}} = {V_{N.CIH}} - {V_{N.EFC'}} - {V_{L.ABH}} - {V_{M.ADI}}$

Ta dễ dàng chứng minh được $B,D$ lần lượt là trung điểm của $CH,CI \Rightarrow BD = \dfrac{1}{2}HI \Rightarrow EF = \dfrac{1}{2}BD = \dfrac{1}{4}HI$

$\Rightarrow \Delta C'EF$ đồng dạng với $\Delta CIH$ theo tỉ số đồng dạng $k = \dfrac{1}{4} \Rightarrow \dfrac{{{S_{\Delta C'EF}}}}{{{S_{\Delta CIH}}}} = \dfrac{1}{{16}}$

 $\begin{array}{l}\dfrac{{NC'}}{{NC}} = \dfrac{{EC'}}{{HC}} = \dfrac{1}{4} \Rightarrow \dfrac{{d\left( {N';\left( {C'EF} \right)} \right)}}{{d\left( {N;\left( {CIH} \right)} \right)}} = \dfrac{1}{4}\\ \Rightarrow {V_{N.EFC'}} = \dfrac{1}{{16}}.\dfrac{1}{4}{V_{N.CIH}} = \dfrac{1}{{64}}{V_{N.CIH}}\\{V_{LABH}} = {V_{M.ADI}} = \dfrac{1}{2}.\dfrac{1}{4}{V_{N.CIH}} = \dfrac{1}{8}{V_{N.CIH}}\\ \Rightarrow {V_{H'}} = {V_{N.CIH}} - {V_{N.EFC'}} - {V_{L.ABH}} - {V_{M.ADI}} = \dfrac{{47}}{{64}}{V_{N.CIH}}\end{array}$

 Ta có :

$\begin{array}{l}\dfrac{{CC'}}{{NC}} = \dfrac{3}{4},\dfrac{{{S_{ABCD}}}}{{{S_{CIH}}}} = \dfrac{1}{2} \Rightarrow \dfrac{{{V_{ABCD.A'B'C'D'}}}}{{{V_{S.CIH}}}} = \dfrac{{d\left( {C';\left( {ABCD} \right)} \right).{S_{ABCD}}}}{{\dfrac{1}{3}d\left( {N;\left( {CIH} \right)} \right).{S_{CIH}}}} = 3.\dfrac{{CC'}}{{NC}}.\dfrac{{{S_{ABCD}}}}{{{S_{CIH}}}} = 3.\dfrac{3}{4}.\dfrac{1}{2} = \dfrac{9}{8}\\ \Rightarrow {V_{S.CIH}} = \dfrac{8}{9}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow {V_{H'}} = \dfrac{{47}}{{64}}{V_{N.CIH}} = \dfrac{{47}}{{72}}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow {V_H} = \dfrac{{25}}{{72}}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow \dfrac{{{V_H}}}{{{V_{H'}}}} = \dfrac{{25}}{{47}}\end{array}$