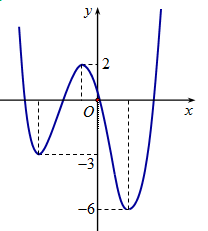
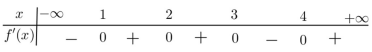Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Đường cong trong hình vẽ bên là đồ thị hàm số \(y = f'\left( x \right)\), (\(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\)). Xét hàm số \(g\left( x \right) = f\left( {{x^2} - 2} \right)\). Mệnh đề nào dưới đây sai?

Từ đồ thị thấy \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 2\end{array} \right.\) và \(f'\left( x \right) > 0 \Leftrightarrow x > 2\).

Xét \(g\left( x \right) = f\left( {{x^2} - 2} \right)\) có TXĐ \(D = \mathbb{R}\).

\(g'\left( x \right) = 2xf'\left( {{x^2} - 2} \right) = 2x.f'\left( t \right)\)  với \(t = {x^2} - 2\)

\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\t = {x^2} - 2 =  - 1\\t = {x^2} - 2 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm 1\\x =  \pm 2\end{array} \right.\)

Có:

\(f'\left( t \right) > 0 \Leftrightarrow t = {x^2} - 2 > 2 \Leftrightarrow \left[ \begin{array}{l}x <  - 2\\x > 2\end{array} \right.\)

\(f'\left( t \right) < 0 \Leftrightarrow t = {x^2} - 2 < 2 \Leftrightarrow  - 2 < x < 2\)

Suy ra:

+) $g'\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\f'\left( t \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\f'\left( t \right) < 0\end{array} \right.\end{array} \right.$ \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\x <  - 2;x > 2\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\ - 2 < x < 2\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x > 2\\ - 2 < x < 0\end{array} \right.\)

+) $g'\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\f'\left( t \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\f'\left( t \right) > 0\end{array} \right.\end{array} \right.$\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\ - 2 < x < 2\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\x > 2;x <  - 2\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}0 < x < 2\\x <  - 2\end{array} \right.\)

Bảng biến thiên:

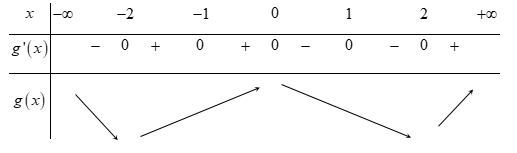
Vậy hàm số \(y = g\left( x \right)\) đồng biến trên các khoảng \(\left( { - 2;0} \right)\) và \(\left( {2; + \infty } \right)\)

Hàm số \(y = g\left( x \right)\) nghịch biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0;2} \right)\)

Vậy C sai.