Câu hỏi:
2 năm trước
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a\), \(AD = 2a\) và \(AA' = 2a\). Tính bán kính \(R\) của mặt cầu ngoại tiếp tứ diện \(ABB'C'\).
Trả lời bởi giáo viên
Đáp án đúng: c
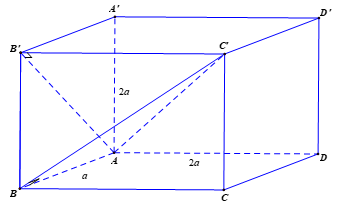
Mặt cầu ngoại tiếp tứ diện \(ABB'C'\) cũng là mặt cầu ngoại tiếp hình hộp chữ nhật \(ABCD.A'B'C'D'\)
Do đó bán kính là \(R = \dfrac{1}{2}\sqrt {{a^2} + {{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}} = \dfrac{{3a}}{2}\).
Hướng dẫn giải:
Mặt cầu ngoại tiếp tứ diện \(ABB'C'\) cũng là mặt cầu ngoại tiếp hình hộp chữ nhật \(ABCD.A'B'C'D'\)

