Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác vuông tại \(A\), \(AB = 2a\sqrt 3 \). Đường chéo \(BC'\) tạo với mặt phẳng \(\left( {AA'C'C} \right)\) một góc bằng \(60^\circ \). Gọi \(\left( S \right)\) là mặt cầu ngoại tiếp hình lăng trụ đã cho. Bán kính của mặt cầu \(\left( S \right)\) bằng
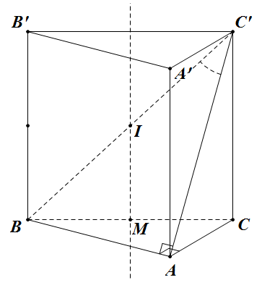
Gọi \(M\) là trung điểm \(BC\), \(I\) là trung điểm \(BC'\). Khi đó, \(IM\) là trục của đường tròn ngoại tiếp tam giác \(ABC\). Mặt khác, \(IB = IC = IB' = IC' = IA'\). Do đó, \(I\) là tâm mặt cầu ngoại tiếp lăng trụ \(ABC.A'B'C'\). Bán kính \(R = \dfrac{1}{2} \cdot BC' = \dfrac{1}{2} \cdot \dfrac{{AB}}{{\sin 60^\circ }} = \dfrac{{4a}}{2} = 2a\).
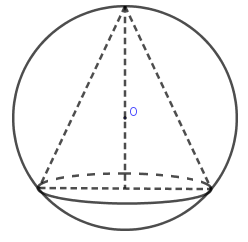
Một hình nón có thiết diện qua trục là tam giác đều cạnh \(a\). Tính bán kính mặt cầu ngoại tiếp hình nón theo \(a\).
Ta có đường cao hình nón \(h = \dfrac{{a\sqrt 3 }}{2}\)\( \Rightarrow R = \dfrac{2}{3}h = \dfrac{{a\sqrt 3 }}{3}\).
Cho hình chóp tam giác \(S.ABC\) có \(\widehat {SAC} = \widehat {SBC} = {90^0}\). Khi đó tâm mặt cầu ngoại tiếp hình chóp nằm trên đường thẳng nào?
Ta thấy: \(\widehat {SAC} = \widehat {SBC} = {90^0}\) nên các đỉnh \(A,B\) luôn nhìn cạnh \(SC\) một góc \({90^0}\). Do đó tâm mặt cầu ngoại tiếp hình chóp là trung điểm \(SC\).
Công thức tính diện tích mặt cầu là:
Công thức tính diện tích mặt cầu \(S = 4\pi {R^2}\)
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có độ dài cạnh đáy bằng \(a\) và chiều cao bằng \(h\). Tính thể tích \(V\) của khối trụ ngoại tiếp lăng trụ đã cho.

Khối trụ ngoại tiếp lăng trụ tam giác đều có hình tròn đáy là hình tròn ngoại tiếp tam giác đáy của lăng trụ, và chiều cao bằng chiều cao lăng trụ.
Tam giác đều cạnh \(a\) có bán kính đường tròn ngoại tiếp bằng \(\dfrac{{\sqrt 3 a}}{3}\). Vậy thể tích của khối trụ cần tìm là \(V = h.S = h.\pi .{\left( {\dfrac{{\sqrt 3 a}}{3}} \right)^2} = \dfrac{{\pi {a^2}h}}{3}\)(đvtt).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\)là hình thoi cạnh \(a\),\(\widehat {ABC} = {120^0}\), tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\).
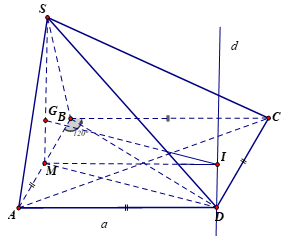
Do \(\widehat {ABC} = 120^\circ \Rightarrow \widehat {BAD} = 60^\circ \) suy ra \(\Delta ABD\) đều
\( \Rightarrow DA = DB = DC = a\) nên \(D\) là tâm đường tròn ngoại tiếp \(\Delta ABC\).
Gọi $M$ là trung điểm của\(AB\), $G$ là trọng tâm của \(\Delta SAB\).
Qua \(D\) kẻ \(d \bot (ABCD)\), và qua \(G\) kẻ \(d' \bot (SAB)\)
Gọi \(I = d \cap d'\).
Ta có \(IA = IB = IC = ID\)
Khi đó \(I\) là tâm của mặt cầu ngoại tiếp hình chóp \(S.ABC\) có bán kính \(R = IA = \sqrt {A{D^2} + M{G^2}} = \sqrt {{a^2} + {{\left( {\dfrac{{a\sqrt 3 }}{6}} \right)}^2}} = \dfrac{{\sqrt {39} }}{6}a\)
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông cạnh \(a\) và cạnh bên bằng \(2a\). Diện tích xung quanh ${S_{xq}}$ của hình nón có đỉnh là tâm \(O\) của hình vuông \(A'B'C'D'\) và đáy là hình tròn nội tiếp hình vuông \(ABCD\) là:
Dựa vào giả thiết ta có bán kính đáy hình nón là bán kính đường tròn nội tiếp hình vuông nên $r = \dfrac{a}{2}$.
Chiều cao hình nón là khoảng cách từ \(O\) đến mặt phẳng \(\left( {ABCD} \right)\)nên $h = 2{\rm{a}}$
Độ dài đường sinh hình nón là $l = \sqrt {{h^2} + {r^2}} = \sqrt {4{{\rm{a}}^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt {17} }}{2}$
Diện tích xung quanh của hình nón là ${S_{xq}} = \pi {\rm{r}}l = \pi \dfrac{a}{2}.\dfrac{{a\sqrt {17} }}{2} = \dfrac{{\pi {a^2}\sqrt {17} }}{4}$.
Một cái cột có hình dạng như hình bên (gồm một khối nón và một khối trụ ghép lại). Chiều cao đo được ghi trên hình, chu vi đáy là \(20\sqrt 3 \pi \) cm. Thể tích của cột bằng:
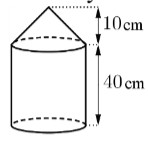
Gọi \(r\) là bán kính đường tròn đáy của hình trụ và hình nón.
Theo bài ra ta có: Chu vi đáy là \(C = 2\pi r = 20\sqrt 3 \pi \Rightarrow r = 10\sqrt 3 \,\,\left( {cm} \right)\)
Thể tích khối nón là \({V_1} = \dfrac{1}{3}\pi {r^2}.{h_1} = \dfrac{1}{3}\pi .{\left( {10\sqrt 3 } \right)^2}.10 = 1000\pi \,\,\left( {c{m^3}} \right)\)
Thể tích khối trụ là \({V_2} = \pi {r^2}.{h_2} = \pi .{\left( {10\sqrt 3 } \right)^2}.40 = 12000\pi \,\,\,\left( {c{m^3}} \right)\)
Thể tích của cột là \(V = {V_1} + {V_2} = 13000\pi \,\,\left( {c{m^3}} \right)\).
Ca (Canxi) có cấu trúc lập phương tâm diện, mỗi nguyên tử Ca có dạng hình cầu bán kính R. Một ô cơ sở của mạng tinh thể Ca là một hình lập phương có cạnh bằng a, mỗi mặt của hình lập phương chứa \(\dfrac{1}{2}\) nguyên tử Ca và mỗi góc chứa \(\dfrac{1}{8}\) nguyên tử Ca khác (Hình a, b)
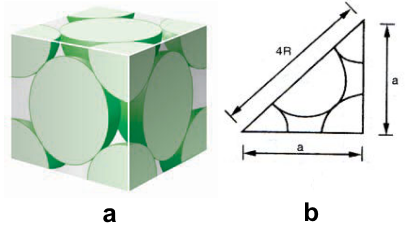
Độ đặc khít của Ca trong một ô cơ sở là tỉ lệ % thể tích mà Ca chiếm chỗ trong ô cơ sở đó. Độ đặc khít của Ca trong một ô cơ sở là:
Bước 1: Tính số nguyên tử Ca có trong một ô cơ sở
Số nguyên tử Ca trong một ô cơ sở gồm: 6 mặt mỗi mặt có \(\dfrac{1}{2}\) khối cầu+8 góc \(\dfrac{1}{8}\) khối cầu. Như thế số nguyên tử Ca là: \(6.\dfrac{1}{2} + 8.\dfrac{1}{8} = 4\) nguyên tử.
Bước 2: Tính thể tích chiếm chỗ của Ca trong một ô cơ sở và thể tích của ô cơ sở.
Thể tích của 4 nguyên tử Ca là: \({V_{Ca}} = 4.\dfrac{4}{3}\pi {R^3} = \dfrac{{16}}{3}\pi {R^3}\)
Thể tích của một khối lập phương là \({V_{lp}} = {a^3}\).
Bước 3: Tính R theo a và độ đặc khít
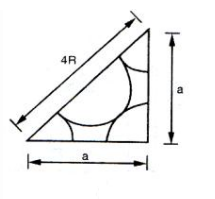
Theo hình vẽ ta thấy cạnh huyền: \(4R\), các cạnh góc vuông đều bằng a.
Theo định lý Pitago ta có:
\({\left( {4R} \right)^2} = {a^2} + {a^2}\)
\(\begin{array}{l} \Leftrightarrow 16{R^2} = 2{a^2} \Leftrightarrow {a^2} = 8{R^2}\\ \Leftrightarrow a = 2R\sqrt 2 \Rightarrow \dfrac{R}{a} = \dfrac{1}{{2\sqrt 2 }}\end{array}\)
\(\begin{array}{l} \Rightarrow \dfrac{{{V_{Ca}}}}{{{V_{lp}}}} = \dfrac{{\dfrac{{16}}{3}\pi .{R^3}}}{{{a^3}}} = \dfrac{{16}}{3}\pi .{\left( {\dfrac{R}{a}} \right)^3}\\ = \dfrac{{16\pi }}{3}.{\left( {\dfrac{1}{{2\sqrt 2 }}} \right)^3} \approx 0,74 = 74\% \end{array}\)

