Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\)là hình thoi cạnh \(a\),\(\widehat {ABC} = {120^0}\), tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\).
Trả lời bởi giáo viên
Đáp án đúng: c
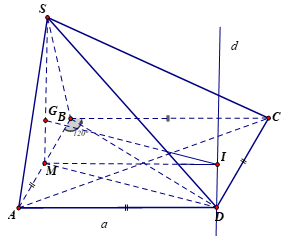
Do \(\widehat {ABC} = 120^\circ \Rightarrow \widehat {BAD} = 60^\circ \) suy ra \(\Delta ABD\) đều
\( \Rightarrow DA = DB = DC = a\) nên \(D\) là tâm đường tròn ngoại tiếp \(\Delta ABC\).
Gọi $M$ là trung điểm của\(AB\), $G$ là trọng tâm của \(\Delta SAB\).
Qua \(D\) kẻ \(d \bot (ABCD)\), và qua \(G\) kẻ \(d' \bot (SAB)\)
Gọi \(I = d \cap d'\).
Ta có \(IA = IB = IC = ID\)
Khi đó \(I\) là tâm của mặt cầu ngoại tiếp hình chóp \(S.ABC\) có bán kính \(R = IA = \sqrt {A{D^2} + M{G^2}} = \sqrt {{a^2} + {{\left( {\dfrac{{a\sqrt 3 }}{6}} \right)}^2}} = \dfrac{{\sqrt {39} }}{6}a\)
Hướng dẫn giải:
- Dựng tâm \(I\) của mặt cầu ngoại tiếp hình chóp \(S.ABC\) (cách đều \(4\) đỉnh)
- Tính bán kính dựa vào các kiến thức đã học ở lớp dưới.
