Ca (Canxi) có cấu trúc lập phương tâm diện, mỗi nguyên tử Ca có dạng hình cầu bán kính R. Một ô cơ sở của mạng tinh thể Ca là một hình lập phương có cạnh bằng a, mỗi mặt của hình lập phương chứa \(\dfrac{1}{2}\) nguyên tử Ca và mỗi góc chứa \(\dfrac{1}{8}\) nguyên tử Ca khác (Hình a, b)
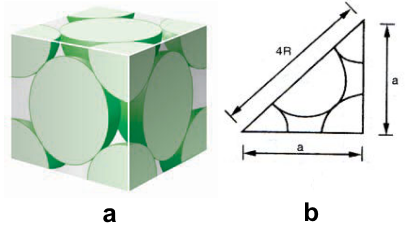
Độ đặc khít của Ca trong một ô cơ sở là tỉ lệ % thể tích mà Ca chiếm chỗ trong ô cơ sở đó. Độ đặc khít của Ca trong một ô cơ sở là:
Trả lời bởi giáo viên
Bước 1: Tính số nguyên tử Ca có trong một ô cơ sở
Số nguyên tử Ca trong một ô cơ sở gồm: 6 mặt mỗi mặt có \(\dfrac{1}{2}\) khối cầu+8 góc \(\dfrac{1}{8}\) khối cầu. Như thế số nguyên tử Ca là: \(6.\dfrac{1}{2} + 8.\dfrac{1}{8} = 4\) nguyên tử.
Bước 2: Tính thể tích chiếm chỗ của Ca trong một ô cơ sở và thể tích của ô cơ sở.
Thể tích của 4 nguyên tử Ca là: \({V_{Ca}} = 4.\dfrac{4}{3}\pi {R^3} = \dfrac{{16}}{3}\pi {R^3}\)
Thể tích của một khối lập phương là \({V_{lp}} = {a^3}\).
Bước 3: Tính R theo a và độ đặc khít
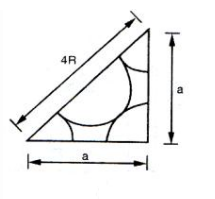
Theo hình vẽ ta thấy cạnh huyền: \(4R\), các cạnh góc vuông đều bằng a.
Theo định lý Pitago ta có:
\({\left( {4R} \right)^2} = {a^2} + {a^2}\)
\(\begin{array}{l} \Leftrightarrow 16{R^2} = 2{a^2} \Leftrightarrow {a^2} = 8{R^2}\\ \Leftrightarrow a = 2R\sqrt 2 \Rightarrow \dfrac{R}{a} = \dfrac{1}{{2\sqrt 2 }}\end{array}\)
\(\begin{array}{l} \Rightarrow \dfrac{{{V_{Ca}}}}{{{V_{lp}}}} = \dfrac{{\dfrac{{16}}{3}\pi .{R^3}}}{{{a^3}}} = \dfrac{{16}}{3}\pi .{\left( {\dfrac{R}{a}} \right)^3}\\ = \dfrac{{16\pi }}{3}.{\left( {\dfrac{1}{{2\sqrt 2 }}} \right)^3} \approx 0,74 = 74\% \end{array}\)
Hướng dẫn giải:
Bước 1: Tính số nguyên tử Ca có trong một ô cơ sở
Bước 2: Tính thể tích chiếm chỗ của Ca trong một ô cơ sở và thể tích của ô cơ sở.
Bước 3: Tính R theo a và độ đặc khít.

