Mặt cầu ngoại tiếp, nội tiếp đa diện

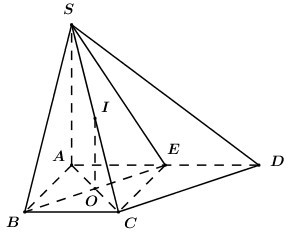
Xét tứ giác \(ABCE\) có \(AB = BC = AE = a,\,\,BC\parallel AE,\,\,\angle ABC = {90^0}\) nên \(ABCE\) là hình vuông.

Gọi \(O = AC \cap BD\), \(I\) là trung điểm của \(SC\) ta có \(OI\parallel SA\) (\(OI\) là đường trung bình của tam giác \(SAC\)) nên \(OI \bot \left( {ABCD} \right)\).

Do đó \(IA = IB = IC = IE\).

Lại có \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A\)  (tam giác vuông có trung điểm của cạnh huyền là tâm đường tròn ngoại tiếp tam giác).

\( \Rightarrow IS = IA = IB = IC = IE\) \( \Rightarrow I\) là tâm mặt cầu đi qua các điểm \(S,\,\,A,\,\,B,\,\,C,\,\,E\), bán kính của khối cầu này là \(R = IS = \dfrac{1}{2}SC\).

Vì  là hình vuông cạnh  nên \(AC = a\sqrt 2 \).

Áp dụng định lí Pytago trong tam giác vuông  có: \(SC = \sqrt {S{A^2} + A{C^2}}  = \sqrt {2{a^2} + 2{a^2}}  = 2a\).

Vậy \(R = \dfrac{1}{2}SC = a\).

Thể tích khối cầu đã cho là: \(V = 4\pi {a^3}\) \( \Leftrightarrow \dfrac{4}{3}\pi {R^3} = 4\pi {a^3}\) \( \Leftrightarrow {R^3} = 3{a^3} \Leftrightarrow R = a\sqrt[3]{3}\)

Bán kính của mặt cầu đã cho là:\(R = 12:2 = 6.\)

Thể tích khối cầu đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.6^3} = 288\pi .\)

Diện tích mặt cầu đã cho là:\(S = 4\pi {r^2} = 4\pi {.6^2} = 144\pi .\)

Diện tích mặt cầu bán kính \(R = 3\) đã cho là: \(S = 4\pi {R^2} = 4\pi {.3^2} = 36\pi .\)

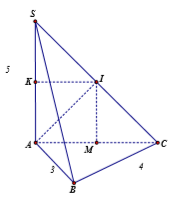
Gọi \(M\) là trung điểm của \(AC\). Vì tam giác \(ABC\) vuông tại \(B\) nên \(M\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)

Qua \(M\) dựng đường thẳng \(d\parallel SA,\,\,d \cap SC = \left\{ I \right\}\), khi đó ta có \(IA = IB = IC\,\,\,\left( 1 \right)\).

Xét tam giác \(SAC\) có: \(M\) là trung điểm \(AC\), \(MI\parallel SA\) \( \Rightarrow I\) là trung điểm của \(SC\) (định lí đường trung bình của tam giác).

Mà \(\Delta SAC\) vuông tại \(C\) nên \(I\) là tâm đường tròn ngoại tiếp \(\Delta SAC\) \( \Rightarrow IA = IC = IS\,\,\left( 2 \right)\).

Từ (1) và (2) \( \Rightarrow IA = IB = IC = IS\) \( \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\), khối cầu này có bán kính \(R = IA\).

Ta có \(IM = \dfrac{1}{2}SA = \dfrac{5}{2}\), \(AM = \dfrac{1}{2}AC = \dfrac{1}{2}\sqrt {{3^2} + {4^2}}  = \dfrac{5}{2}\).

Áp dụng định lí Pytago trong tam giác vuông \(AIM\) có:

\(R = IA = \sqrt {A{M^2} + I{M^2}}  = \sqrt {\dfrac{{25}}{4} + \dfrac{{25}}{4}}  = \dfrac{{5\sqrt 2 }}{2}\)

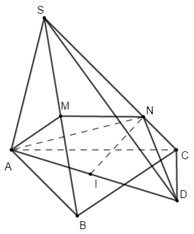
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC.

Kẻ đường kính AD của đường tròn tâm I.

Khi đó  \(\left\{ \begin{array}{l}C \in \left( {I;r} \right) \Rightarrow AC \bot CD\\SA \bot CD\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right)\)

\(\begin{array}{l} \Rightarrow CD \bot AN;AN \bot SC\\ \Rightarrow AN \bot \left( {SCD} \right)\\ \Rightarrow AN \bot DN\end{array}\)

\( \Rightarrow \angle AND = 90^\circ \)

Nên N thuộc đường tròn \(\left( {I;r} \right)\)

Tương tự ta có M thuộc đường tròn \(\left( {I;r} \right)\)

Vậy mặt cầu ngoại tiếp ABCNM là mặt cầu \(\left( {I;r} \right)\) \( \Rightarrow r = IA\).

Ta có \(2r = \frac{{BC}}{{\sin BAC}} = \frac{{\sqrt 7 }}{{\sin 60^\circ }} \Rightarrow r = \frac{{\sqrt {21} }}{3}\).

Gọi bán kính là \(R\)

Ta có: \(V = \dfrac{{32\pi {a^3}}}{3}\)  nên \(\dfrac{4}{3}\pi {R^3} = \dfrac{{32}}{3}\pi {a^3}\)\( \Leftrightarrow {R^3} = 8{a^3} \Leftrightarrow R = 2a\)

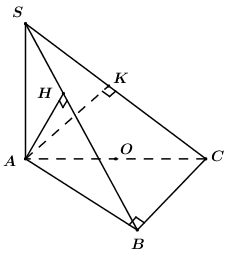
Gọi \(O\) là trung điểm của \(AC\).

Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\).

Ta có: \(\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot HC\) \( \Rightarrow \Delta AHC\) vuông tại \(H\) \( \Rightarrow H\) thuộc mặt cầu tâm \(O\) đường kính \(AC\).

Ta lại có: \(\Delta AKC,\,\,\Delta ABC\) lần lượt vuông tại \(K,\,\,B\) \( \Rightarrow K,\,\,B\) thuộc thuộc mặt cầu tâm \(O\) đường kính \(AC\).

\( \Rightarrow \) 5 điểm \(A,\,\,H,\,\,K,\,\,B,\,\,C\) đều thuộc mặt cầu tâm \(O\) đường kính AC hay khối chóp \(A.HKCB\) nội tiếp mặt cầu tâm \(O\) đường kính \(AC\). Khi đó bán kính mặt cầu là \(R = \dfrac{{AC}}{2}\).

Tam giác \(ABC\) vuông cân tại \(B\) và \(BC = a \Rightarrow AC = a\sqrt 2 \)\( \Rightarrow R = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\).

Vậy thể tích của khối cầu ngoại tiếp hình chóp \(A.HKCB\) bằng \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^3} = \dfrac{{\pi {a^3}\sqrt 2 }}{3}\).

Theo đề bài ta có: \(V = 36\pi \) \( \Leftrightarrow \frac{4}{3}\pi {R^3} = 36\pi \)\( \Leftrightarrow {R^3} = 27\)\( \Leftrightarrow R = 3\)

Diện tích mặt cầu đã cho là: \(S = 4\pi {R^2} = 4\pi {.3^2} = 36\pi .\)

Diện tích mặt cầu có bán kính \(r\) bằng \(4\pi {r^2}\).

Tăng bán kính mặt cầu lên 4 lần thì diện tích mặt cầu tăng 16 lần.

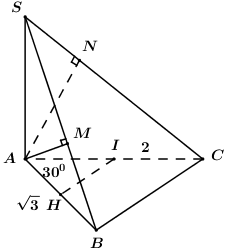
Áp dụng định lí Cosin trong tam giác ABC ta có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \angle BAC\\B{C^2} = {\left( {\sqrt 3 } \right)^2} + {2^2} - 2.\sqrt 3 .2.\dfrac{{\sqrt 3 }}{2} = 1\\ \Rightarrow BC = 1\\ \Rightarrow A{B^2} + B{C^2} = A{C^2}\end{array}\)

\( \Rightarrow \Delta ABC\) vuông tại B (Định lí Pytago đảo).

Gọi I là trung điểm của AC \( \Rightarrow I\) là tâm đường tròn ngoại tiếp tam giác ABC, do đó có IA = IB = IC  (1).

Gọi H là trung điểm của AB ta có: \(IH \bot AB\).

Ta có: \(\left\{ \begin{array}{l}IH \bot AB\\IH \bot SA\end{array} \right. \Rightarrow IH \bot \left( {SAB} \right) \Rightarrow IH \bot \left( {ABM} \right)\).

Lại có \(\Delta ABM\) vuông tại M, có H là trung điểm của cạnh huyền AB nên H là tâm đường tròn ngoại tiếp \(\Delta ABM\) \( \Rightarrow IH\) là trục của \(\left( {ABM} \right)\) \( \Rightarrow IA = IB = IM\)  (2).

\(\Delta ACN\) vuông tại N có I là trung điểm cạnh huyền BC nên IA = IC = IN (3)

Từ (1), (2), (3) ta suy ra IA = IB = IC = IM = IN hay I là tâm mặt cầu ngoại tiếp khối chóp A.BCNM, bán kính khối cầu là R = IA \( = \dfrac{1}{2}AC = 1\).

Thể tích khối cầu có bán kính \(r = a\) là: \({V_1} = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {a^3}.\)

Thể tích khối cầu có bán kính \(R = 2a\) là: \({V_2} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {2a} \right)^3} = \frac{{32}}{3}\pi {a^3}.\)

\( \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{4}{3}\pi {a^3}}}{{\frac{{32}}{3}\pi {a^3}}} = \frac{4}{{32}} = \frac{1}{8}.\)

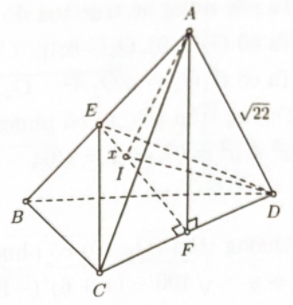
+) Gọi E, F lần lượt là trung điểm của AB, CD

Ta có  tam giác ACD cân tại \(A\) có trung tuyến \(AF\)\( \Rightarrow AF \bot CD\)

 cân tại \(B\) có trung tuyến \(BF \Rightarrow BF \bot CD\).

 \( \Rightarrow CD \bot (AFB) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{CD \bot AB}\\{CD \bot EF}\end{array}} \right.\)

Mặt khác vì \(\Delta ACD = \Delta BCD\) (c.c.c) \( \Rightarrow AF = BF \Rightarrow EF \bot AB\).

\( \Rightarrow EF\) là đoạn vuông góc chung của AB và CD.

Do đó EF là trung trực của AB và CD nên tâm mặt cầu ngoại tiếp tứ diện ABCD là điểm \(I\) thuộc đoạn EF

+) Trong tam giác vuông \(ADF \cdot A{F^2} = A{D^2} - D{F^2} = 18\)\( \Rightarrow AF = 3\sqrt 2 \).

\({V_{ABCD}} = 2{V_{DABF}} = 2 \cdot \dfrac{1}{3}DF \cdot {S_{ABF}}\)\( = \dfrac{2}{3}DF\dfrac{1}{2} \cdot AF \cdot BF\sin \widehat {AFB}\) \( \le \dfrac{1}{3}DF \cdot AF \cdot BF = \dfrac{1}{3} \cdot {(3\sqrt 2 )^2} = 6.\)

\({V_{ABCD}}\) lớn nhất bằng 6 khi \(\sin \widehat {AFB} = 1 \Leftrightarrow \widehat {AFB} = {90^0 }\)\( \Leftrightarrow AF \bot BF\).

+) Trong tam giác vuông cân ABF có: \(AB = AF\sqrt 2  = 6 \Rightarrow EF = 3\).

Đặt \(IE = x \Rightarrow IF = 3 - x(0 \le x \le 3)\)

Trong tam giác vuông AEI có: \(A{I^2} = {x^2} + 9\).

Trong tam giác vuông DFI có: \(D{I^2} = {(3 - x)^2} + 4\).

Tứ diện ABCD ngoại tiếp mặt cầu tâm \(I\) thì \(R = AI = DI \Rightarrow A{I^2} = D{I^2}\)

\( \Rightarrow {x^2} + 9 = {(3 - x)^2} + 4\)\( \Leftrightarrow  - 6x + 4 = 0 \Leftrightarrow x = \dfrac{2}{3}\)\( \Rightarrow {R^2} = A{I^2} = \dfrac{{85}}{9}\)

Vậy \(S = 4\pi {R^2} = 4\pi  \cdot \dfrac{{85}}{9} = \dfrac{{340\pi }}{9}\).

Diện tích của mặt cầu bán kính \(R = 3\) bằng \(S = 4\pi {.3^2} = 36\pi \).

Thể tích khối cầu đã cho là: \(V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32\pi }}{3}.\)

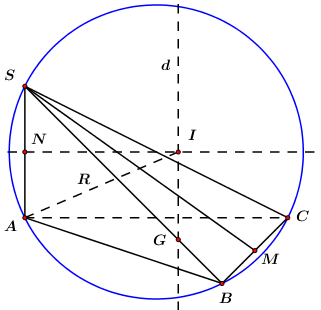
Gọi \(G\) là trọng tâm \(\Delta ABC\)

Ta có: \(SA \bot \left( {ABC} \right)\)

Qua \(G,\) dựng đường thẳng \(d\) song song với \(SA\) \( \Rightarrow d \bot \left( {ABC} \right)\)

Dựng đường trung trực của \(SA,\) cắt \(d\) tại \(I\) \( \Rightarrow I\) là tâm mặt cầu ngoại tiếp khối \(SABC.\)

\( \Rightarrow R = AI.\)

Gọi \(M,\,\,N\) lần lượt là trung điểm của \(BC\) và \(SA.\)

Ta có: \(\Delta ABC\) đều \( \Rightarrow AM \bot BC\) (tính chất tam giác đều).

Lại có: \(\Delta SBC\) cân tại \(S\) \( \Rightarrow SM \bot BC = \left\{ M \right\}\) (tính chất tam giác cân)

\( \Rightarrow \angle \left( {\left( {SBC} \right),\,\,\left( {ABC} \right)} \right) = \angle \left( {SM,\,\,AM} \right) = \angle SMA = {30^0}\)

\( \Rightarrow SA = AM.\tan {30^0} = \dfrac{{2a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{3} = a.\)

Có \(AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{2a\sqrt 3 }}{2} = \dfrac{{2a\sqrt 3 }}{3}.\)

Ta có: \(ANIG\) là hình chữ nhật \( \Rightarrow AN = IG = \dfrac{1}{2}SA = \dfrac{a}{2}.\)

Áp dụng định lý Pitago cho \(\Delta AIG\) vuông tại \(G\) ta có:

\(R = AI = \sqrt {A{G^2} + G{I^2}} \) \( = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{2a\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{a\sqrt {57} }}{6}.\)

\( \Rightarrow \) Diện tích mặt cầu ngoại tiếp hình chóp \(SABC\) là: \(S = 4\pi {R^2} = 4\pi .{\left( {\dfrac{{a\sqrt {57} }}{6}} \right)^2} = \dfrac{{19\pi {a^2}}}{3}.\)

Mặt cầu ngoại tiếp hình đa diện nếu nó đi qua mọi đỉnh của đa diện.

Trục đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.