Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) và \(BC = a.\) Cạnh bên \(SA\) vuông góc với đáy \(\left( {ABC} \right).\) Gọi \(H,{\rm{ }}K\) lần lượt là hình chiếu vuông góc của \(A\) lên \(SB\) và \(SC.\) Thể tích của khối cầu ngoại tiếp hình chóp \(A.HKCB\) bằng

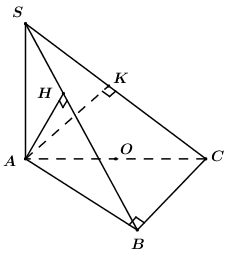
Gọi \(O\) là trung điểm của \(AC\).

Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\).

Ta có: \(\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot HC\) \( \Rightarrow \Delta AHC\) vuông tại \(H\) \( \Rightarrow H\) thuộc mặt cầu tâm \(O\) đường kính \(AC\).

Ta lại có: \(\Delta AKC,\,\,\Delta ABC\) lần lượt vuông tại \(K,\,\,B\) \( \Rightarrow K,\,\,B\) thuộc thuộc mặt cầu tâm \(O\) đường kính \(AC\).

\( \Rightarrow \) 5 điểm \(A,\,\,H,\,\,K,\,\,B,\,\,C\) đều thuộc mặt cầu tâm \(O\) đường kính AC hay khối chóp \(A.HKCB\) nội tiếp mặt cầu tâm \(O\) đường kính \(AC\). Khi đó bán kính mặt cầu là \(R = \dfrac{{AC}}{2}\).

Tam giác \(ABC\) vuông cân tại \(B\) và \(BC = a \Rightarrow AC = a\sqrt 2 \)\( \Rightarrow R = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\).

Vậy thể tích của khối cầu ngoại tiếp hình chóp \(A.HKCB\) bằng \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^3} = \dfrac{{\pi {a^3}\sqrt 2 }}{3}\).