Tập hợp các điểm cách đều hai đầu mút của đoạn thẳng là:
Mọi điểm nằm trên mặt phẳng trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng và ngược lại.
Hình nào sau đây không có mặt cầu ngoại tiếp?
- Hình hộp chữ nhật và hình lập phương đều có mặt cầu ngoại tiếp nên A và B đúng.
- Hình lăng trụ đứng có đáy là đa giác nội tiếp được đường tròn thì có mặt cầu ngoại tiếp nên C đúng.
- Hình chóp có đáy là đa giác nội tiếp được đường tròn thì có mặt cầu ngoại tiếp nên D sai vì hình thoi không nội tiếp được đường tròn.
Số mặt cầu ngoại tiếp tứ diện là:
Vì tứ diện là hình chóp tam giác nên nó luôn có mặt cầu ngoại tiếp, ngoài ra nó chỉ có duy nhất một mặt cầu ngoại tiếp.
Hình chóp nào sau đây luôn nội tiếp được mặt cầu?
Trong các hình chóp tam giác, tứ giác, ngũ giác, lục giác thì chỉ có tam giác luôn nội tiếp được đường tròn nên hình chóp tam giác luôn nội tiếp được mặt cầu.
Cho hình chóp tam giác \(S.ABC\) có \(\widehat {SAC} = \widehat {SBC} = {90^0}\). Khi đó tâm mặt cầu ngoại tiếp hình chóp nằm trên đường thẳng nào?
Ta thấy: \(\widehat {SAC} = \widehat {SBC} = {90^0}\) nên các đỉnh \(A,B\) luôn nhìn cạnh \(SC\) một góc \({90^0}\). Do đó tâm mặt cầu ngoại tiếp hình chóp là trung điểm \(SC\).
Tâm mặt cầu ngoại tiếp hình chóp tam giác đều nằm ở đâu?
Tâm mặt cầu ngoại tiếp hình chóp tam giác đều nằm trên đoạn nối đỉnh với tâm đáy.
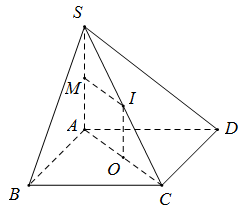
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(a\), cạnh bên \(b\). Công thức tính bán kính mặt cầu ngoại tiếp khối chóp là:
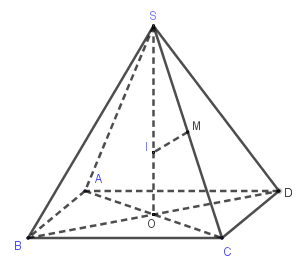
Ta có: \(ABCD\) là hình vuông cạnh \(a\) nên \(AC = a\sqrt 2 \Rightarrow OA = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\)
Tam giác \(SOC\) vuông tại \(O\) nên \(S{C^2} = S{O^2} + O{C^2} \Rightarrow h = SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{b^2} - \dfrac{{{a^2}}}{2}} \)
Vậy \(R = \dfrac{{{b^2}}}{{2h}} = \dfrac{{{b^2}}}{{2\sqrt {{b^2} - \dfrac{{{a^2}}}{2}} }}\)
Công thức tính bán kính mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy là:
Hình chóp có cạnh bên vuông góc với đáy nội tiếp mặt cầu có bán kính \(R = \sqrt {{r^2} + \dfrac{{{h^2}}}{4}} \), với \(r\) là bán kính đường tròn đáy, \(h\) là chiều cao hình chóp (độ dài cạnh bên vuông góc với đáy).
Công thức tính diện tích mặt cầu là:
Công thức tính diện tích mặt cầu \(S = 4\pi {R^2}\)
Khối cầu thể tích \(V\) thì bán kính là:
Ta có: thể tích khối cầu \(V = \dfrac{4}{3}\pi {R^3} \Rightarrow R = \sqrt[3]{{\dfrac{{3V}}{{4\pi }}}}\)
Ba đoạn thẳng $SA,SB,SC$ đôi một vuông góc tạo với nhau thành một tứ diện $SABC$ với $SA = a,SB = 2a,SC = 3a$ . Tính bán kính mặt cầu ngoại tiếp hình tứ diện đó là
Bán kính mặt cầu ngoại tiếp tứ diện vuông $S.ABC$ được tính theo công thức
$R = \sqrt {\dfrac{{S{A^2} + S{B^2} + S{C^2}}}{4}} = \dfrac{{\sqrt {{a^2} + {{\left( {2a} \right)}^2} + {{\left( {3a} \right)}^2}} }}{2} = \dfrac{{a\sqrt {14} }}{2}$
Hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$ có $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$ và có $SA = a,AB = b,AC = c$. Mặt cầu đi qua các đỉnh $A,B,C,S$ có bán kính $r$ bằng :
Vì \(SA \bot \left( {ABC} \right) \Rightarrow \left\{ \begin{array}{l}SA \bot AB\\SA \bot AC\end{array} \right.\).
Mà \(AB \bot AC\) nên hình chóp \(S.ABC\) là tứ diện vuông.
Áp dụng công thức tính bán kính mặt cầu ngoại tiếp tứ diện vuông ta được \(R = \sqrt {\dfrac{{{a^2} + {b^2} + {c^2}}}{4}} = \dfrac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2}\)
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh bằng $1$, mặt bên $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích $V$ của khối cầu ngoại tiếp hình chóp đã cho.
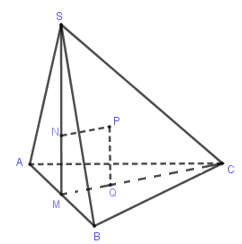
Gọi $M,N,P,Q$ lần lượt là trung điểm $AB$, tâm đường tròn ngoại tiếp $\Delta SAB$, tâm mặt cầu ngoại tiếp hình chóp và tâm đường tròn ngoại tiếp $\Delta ABC \Rightarrow MNPQ$ là hình vuông suy ra
$PN = MQ = \dfrac{1}{3}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{6};NB = \dfrac{2}{3}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{3}$
Bán kính mặt cầu ngoại tiếp chóp là $R = PB = \sqrt {P{N^2} + N{B^2}} = \dfrac{{\sqrt {15} }}{6}$
Thể tích $V = \dfrac{4}{3}\pi {R^3} = \dfrac{{5\sqrt {15} \pi }}{{54}}$
Cho hình chóp tam giác đều $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh \(SA = \dfrac{{2a\sqrt 3 }}{3}\) . Gọi $D$ là điểm đối xứng của $B$ qua $C$. Tính bán kính $R$ của mặt cầu ngoại tiếp hình chóp $S.ABD$
Do $D$ đối xứng với $C$ qua $B$ nên có $BC = DC = AC$ suy ra tam giác $ABD$ là tam giác vuông tại $A$.
Kẻ đường thẳng $d$ qua $C$ vuông góc với đáy, đường thẳng này là trục đường tròn ngoại tiếp tam giác đáy $ABD$ .
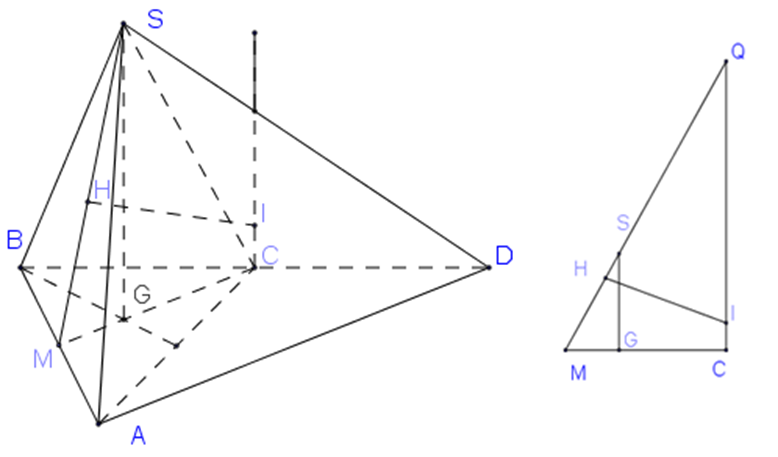
Tam giác $SAB$ cân tại $S$ , gọi $M$ là trung điểm $AB,H$ là tâm đường tròn ngoại tiếp tam giác $SAB$
\( \Rightarrow H \in SM;SM = \sqrt {S{A^2} - A{M^2}} = \dfrac{{a\sqrt {13} }}{{2\sqrt 3 }}\)
\(SH = \dfrac{{AB.SA.SB}}{{4.{S_{SAB}}}} = \dfrac{{{{\left( {\dfrac{{2a}}{{\sqrt 3 }}} \right)}^2}.a}}{{4.\dfrac{1}{2}.a.AM}} = \dfrac{{4a}}{{\sqrt {39} }}\)
Trong $\left( {SAC} \right)$ dựng\(HI \bot SM\left( {I \in d} \right)(1)\).
Mà \(\left\{ \begin{array}{l}AB \bot SM\\AB \bot MC\end{array} \right. \Rightarrow AB \bot \left( {SMC} \right) \Rightarrow AB \bot HI(2)\)
Từ (1), (2) suy ra \(HI \bot \left( {SAB} \right)\) , suy ra $I$ là tâm đường tròn ngoại tiếp hình chóp $S.ABD$
Gọi \(Q = MS \cap CI\), xét tam giác $SCM$ có
\(\dfrac{{SM}}{{QM}} = \dfrac{{MG}}{{MC}} = \dfrac{1}{3}\) \( \Rightarrow QM = 3SM = 3.\dfrac{{a\sqrt {13} }}{{2\sqrt 3 }} = \dfrac{{a\sqrt {39} }}{2}\)
\( \Rightarrow QH = QM - MS + HS\) \( = \dfrac{{a\sqrt {39} }}{2} - \dfrac{{a\sqrt {13} }}{{2\sqrt 3 }} + \dfrac{{4a}}{{\sqrt {39} }} = \dfrac{{17a}}{{\sqrt {39} }}\)
\(QC = \sqrt {Q{M^2} - M{C^2}} = 3a\)
Xét: \(\Delta QHI \sim \Delta QCM \Rightarrow \dfrac{{HI}}{{CM}} = \dfrac{{HQ}}{{QC}}\) \( \Rightarrow HI = \dfrac{{HQ.CM}}{{QC}} = \dfrac{{17a}}{{6\sqrt {13} }}\)
\( \Rightarrow R = SI = \sqrt {H{I^2} + H{S^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt {17} }}{{6\sqrt {13} }}} \right)}^2} + {{\left( {\dfrac{{4a}}{{\sqrt {39} }}} \right)}^2}} = \dfrac{{a\sqrt {37} }}{6}\)
Cho tứ diện đều $ABCD$ có cạnh $a$. Một mặt cầu tiếp xúc với các mặt của tứ diện có bán kính là:
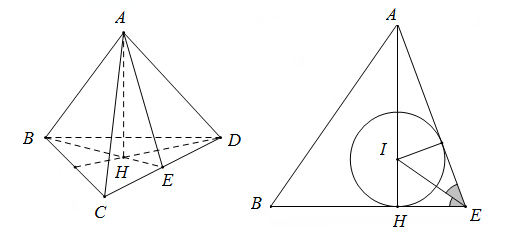
Gọi $H$ là tâm tam giác đều $BCD,E$ là trung điểm $CD$
Ta có $AH \bot \left( {BCD} \right)$
Gọi $I,r$ là tâm và bán kính mặt cầu tiếp xúc với các mặt của tứ diện $ABCD$ thì $I$ là giao của $AH$ và phân giác góc $AEB$ của $\Delta AEB$. Ta có
$\begin{array}{l}AE = BE = \dfrac{{a\sqrt 3 }}{2};HE = \dfrac{{BE}}{3} = \dfrac{{a\sqrt 3 }}{6}\\AH = \sqrt {A{E^2} - H{E^2}} = \dfrac{{a\sqrt 6 }}{3}\end{array}$
Áp dụng tính chất đường phân giác:
$\begin{array}{l}\dfrac{{IH}}{{IA}} = \dfrac{{EH}}{{EA}} \Rightarrow \dfrac{{IH}}{{IH + IA}} = \dfrac{{EH}}{{EH + EA}}\\ \Rightarrow r = IH = \dfrac{{EH.AH}}{{EH + EA}} = \dfrac{{a\sqrt 6 }}{{12}}\end{array}$
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,\,AD = 2a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = 2a\). Tính thể tích khối cầu ngoại tiếp hình chóp \(S.ABCD\).
Gọi $O$ là tâm hình chữ nhật $ABCD,M$ và $I$ lần lượt là trung điểm $SA,SC \Rightarrow AOIM$ là hình chữ nhật.
Ta có $O$ là tâm đường tròn ngoại tiếp hình chữ nhật $ABCD,OI \bot \left( {ABCD} \right)$ nên $OI$ là trục đường tròn ngoại tiếp hình chữ nhật $ABCD$
$IM \bot SA \Rightarrow IM$ là trung trực $SA$ trong mặt phẳng $\left( {SAC} \right)$
$ \Rightarrow I$ là tâm mặt cầu ngoại tiếp hình chóp.
Có $OI = AM = \dfrac{{SA}}{2} = a;OC = \dfrac{{AC}}{2} = \dfrac{1}{2}\sqrt {A{B^2} + A{D^2}} = \dfrac{{a\sqrt 5 }}{2}$
Bán kính và thể tích mặt cầu lần lượt là
$\begin{array}{l}R = IC = \sqrt {I{O^2} + O{C^2}} = \dfrac{{3a}}{2}\\V = \dfrac{4}{3}\pi {R^3} = \dfrac{{9\pi {a^3}}}{2}\end{array}$
Cho lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác vuông cân đỉnh $A,AB = AC = a,AA' = a\sqrt 2 $. Diện tích mặt cầu ngoại tiếp tứ diện $CA'B'C'$ là:
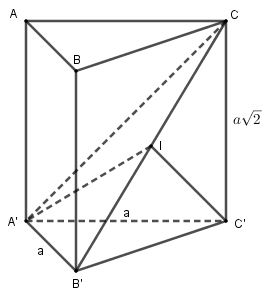
Ta có:
\(\begin{array}{l}A'B' = AB = a\\B'C' = \sqrt {A'B{'^2} + A'C{'^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \\B'C = \sqrt {B'C{'^2} + C'{C^2}} = \sqrt {2{a^2} + 2{a^2}} = 2a\\A'C = \sqrt {A'C{'^2} + C'{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 \\ \Rightarrow A'B{'^2} + A'{C^2} = {a^2} + 3{a^2} = 4{a^2} = B'{C^2}\end{array}\)
\( \Rightarrow \Delta A'B'C\) vuông tại \(A'\).
Gọi \(I\) là trung điểm của \(B'C\) thì \(IB' = IC = IA'\)
Mà \(\Delta CC'B'\) vuông tại \(C'\) nên \(IB' = IC = IC'\)
Vậy \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(CA'B'C'\) và bán kính \(R = \frac{1}{2}B'C = a\).
\( \Rightarrow S = 4\pi {R^2} = 4\pi {a^2}\).
Cho hình chóp $S.ABC$ có $SA \bot (ABC);AC = b,AB = c,\widehat {BAC} = \alpha $. Gọi $B',C'$ lần lượt là hình chiếu vuông góc của $A$ lên $SB,SC$. Tính bán kính mặt cầu ngoại tiếp khối chóp $A.{\rm{ }}BCC'B'$ theo $b,c,\alpha $
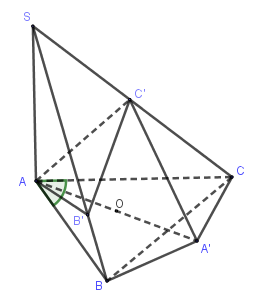
Gọi $AA'$ là đường kính của đường tròn ngoại tiếp tam giác $ABC$
\(AC \bot A'C;\,AB \bot A'B\)
Ta chứng minh \(AC' \bot A'C'\)
\(SA \bot A'C;\,AC \bot A'C \Rightarrow A'C \bot AC'\)
Mà \(AC' \bot SC \Rightarrow AC' \bot A'C'\)
Tương tự \(AB' \bot A'B'\)
Như vậy $B,C,C',B'$ cùng nhìn $AA'$ bằng $1$ góc vuông nên $A,B,C,B',C'$ cùng thuộc $1$ mặt cầu có đường kính là $AA'$ và cũng đồng thời là đường kính của đường tròn ngoại tiếp tam giác $ABC$.
Tính \(BC = \sqrt {{b^2} + {c^2} - 2b\cos \alpha } \)
Trong tam giác \(ABC:\dfrac{{BC}}{{\sin A}} = 2R \Rightarrow R = \dfrac{{\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{2\sin \alpha }}\)
Một hình hộp chữ nhật có độ dài ba cạnh lần lượt là $2;2;1$. Tìm bán kính $R$ của mặt cầu ngoại tiếp hình hộp chữ nhật trên.
Áp dụng công thức trên có $R = \dfrac{3}{2}$
Cho một mặt cầu bán kính bằng $1$. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?
Áp dụng các công thức trong tứ diện đều cạnh $a$
Bán kính mặt cầu nội tiếp $r = \dfrac{{a\sqrt 6 }}{{12}} = 1 \Rightarrow a = 2\sqrt 6 $
Thể tích tứ diện đều đó là $V = \dfrac{{{a^3}\sqrt 2 }}{{12}} = 8\sqrt 3 $

