Cho hình chóp có \(SA \bot \left( {ABC} \right),\) \(AB = 3,\,\,AC = 2,\,\,\angle BAC = 60^\circ \). Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu ngoại tiếp chóp ABCNM.

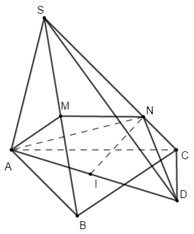
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC.

Kẻ đường kính AD của đường tròn tâm I.

Khi đó  \(\left\{ \begin{array}{l}C \in \left( {I;r} \right) \Rightarrow AC \bot CD\\SA \bot CD\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right)\)

\(\begin{array}{l} \Rightarrow CD \bot AN;AN \bot SC\\ \Rightarrow AN \bot \left( {SCD} \right)\\ \Rightarrow AN \bot DN\end{array}\)

\( \Rightarrow \angle AND = 90^\circ \)

Nên N thuộc đường tròn \(\left( {I;r} \right)\)

Tương tự ta có M thuộc đường tròn \(\left( {I;r} \right)\)

Vậy mặt cầu ngoại tiếp ABCNM là mặt cầu \(\left( {I;r} \right)\) \( \Rightarrow r = IA\).

Ta có \(2r = \frac{{BC}}{{\sin BAC}} = \frac{{\sqrt 7 }}{{\sin 60^\circ }} \Rightarrow r = \frac{{\sqrt {21} }}{3}\).