Xét khối tứ diện ABCD có độ dài cạnh AB thay đổi, \(CD = 4\) và các cạnh còn lại đều bằng \(\sqrt {22} \). Giả sử thể tích khối tứ diện ABCD đạt giá trị lớn nhất, tính diện tích \(S\) của mặt cầu ngoại tiếp tứ diện đó.

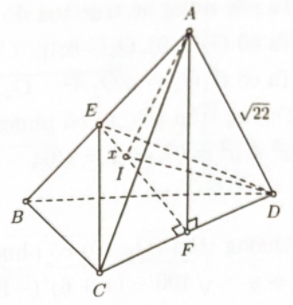
+) Gọi E, F lần lượt là trung điểm của AB, CD

Ta có  tam giác ACD cân tại \(A\) có trung tuyến \(AF\)\( \Rightarrow AF \bot CD\)

 cân tại \(B\) có trung tuyến \(BF \Rightarrow BF \bot CD\).

 \( \Rightarrow CD \bot (AFB) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{CD \bot AB}\\{CD \bot EF}\end{array}} \right.\)

Mặt khác vì \(\Delta ACD = \Delta BCD\) (c.c.c) \( \Rightarrow AF = BF \Rightarrow EF \bot AB\).

\( \Rightarrow EF\) là đoạn vuông góc chung của AB và CD.

Do đó EF là trung trực của AB và CD nên tâm mặt cầu ngoại tiếp tứ diện ABCD là điểm \(I\) thuộc đoạn EF

+) Trong tam giác vuông \(ADF \cdot A{F^2} = A{D^2} - D{F^2} = 18\)\( \Rightarrow AF = 3\sqrt 2 \).

\({V_{ABCD}} = 2{V_{DABF}} = 2 \cdot \dfrac{1}{3}DF \cdot {S_{ABF}}\)\( = \dfrac{2}{3}DF\dfrac{1}{2} \cdot AF \cdot BF\sin \widehat {AFB}\) \( \le \dfrac{1}{3}DF \cdot AF \cdot BF = \dfrac{1}{3} \cdot {(3\sqrt 2 )^2} = 6.\)

\({V_{ABCD}}\) lớn nhất bằng 6 khi \(\sin \widehat {AFB} = 1 \Leftrightarrow \widehat {AFB} = {90^0 }\)\( \Leftrightarrow AF \bot BF\).

+) Trong tam giác vuông cân ABF có: \(AB = AF\sqrt 2  = 6 \Rightarrow EF = 3\).

Đặt \(IE = x \Rightarrow IF = 3 - x(0 \le x \le 3)\)

Trong tam giác vuông AEI có: \(A{I^2} = {x^2} + 9\).

Trong tam giác vuông DFI có: \(D{I^2} = {(3 - x)^2} + 4\).

Tứ diện ABCD ngoại tiếp mặt cầu tâm \(I\) thì \(R = AI = DI \Rightarrow A{I^2} = D{I^2}\)

\( \Rightarrow {x^2} + 9 = {(3 - x)^2} + 4\)\( \Leftrightarrow  - 6x + 4 = 0 \Leftrightarrow x = \dfrac{2}{3}\)\( \Rightarrow {R^2} = A{I^2} = \dfrac{{85}}{9}\)

Vậy \(S = 4\pi {R^2} = 4\pi  \cdot \dfrac{{85}}{9} = \dfrac{{340\pi }}{9}\).