Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(B\), \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = 5\), \(AB = 3\), \(BC = 4\). Bán kính \(R\) của mặt cầu ngoại tiếp hình chóp \(S.ABC\) bằng:

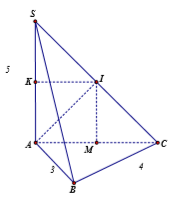
Gọi \(M\) là trung điểm của \(AC\). Vì tam giác \(ABC\) vuông tại \(B\) nên \(M\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)

Qua \(M\) dựng đường thẳng \(d\parallel SA,\,\,d \cap SC = \left\{ I \right\}\), khi đó ta có \(IA = IB = IC\,\,\,\left( 1 \right)\).

Xét tam giác \(SAC\) có: \(M\) là trung điểm \(AC\), \(MI\parallel SA\) \( \Rightarrow I\) là trung điểm của \(SC\) (định lí đường trung bình của tam giác).

Mà \(\Delta SAC\) vuông tại \(C\) nên \(I\) là tâm đường tròn ngoại tiếp \(\Delta SAC\) \( \Rightarrow IA = IC = IS\,\,\left( 2 \right)\).

Từ (1) và (2) \( \Rightarrow IA = IB = IC = IS\) \( \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\), khối cầu này có bán kính \(R = IA\).

Ta có \(IM = \dfrac{1}{2}SA = \dfrac{5}{2}\), \(AM = \dfrac{1}{2}AC = \dfrac{1}{2}\sqrt {{3^2} + {4^2}}  = \dfrac{5}{2}\).

Áp dụng định lí Pytago trong tam giác vuông \(AIM\) có:

\(R = IA = \sqrt {A{M^2} + I{M^2}}  = \sqrt {\dfrac{{25}}{4} + \dfrac{{25}}{4}}  = \dfrac{{5\sqrt 2 }}{2}\)