Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại \(A\) và \(B\). Biết \(SA\) vuông góc với \(\left( {ABCD} \right)\), \(AB = BC = a\), \(AD = 2a\), \(SA = a\sqrt 2 \). Gọi \(E\) là trung điểm của \(AD\). Bán kính mặt cầu đi qua các điểm \(S,\,\,A,\,\,B,\,\,C,\,\,E\) bằng:

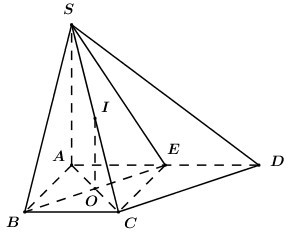
Xét tứ giác \(ABCE\) có \(AB = BC = AE = a,\,\,BC\parallel AE,\,\,\angle ABC = {90^0}\) nên \(ABCE\) là hình vuông.

Gọi \(O = AC \cap BD\), \(I\) là trung điểm của \(SC\) ta có \(OI\parallel SA\) (\(OI\) là đường trung bình của tam giác \(SAC\)) nên \(OI \bot \left( {ABCD} \right)\).

Do đó \(IA = IB = IC = IE\).

Lại có \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A\)  (tam giác vuông có trung điểm của cạnh huyền là tâm đường tròn ngoại tiếp tam giác).

\( \Rightarrow IS = IA = IB = IC = IE\) \( \Rightarrow I\) là tâm mặt cầu đi qua các điểm \(S,\,\,A,\,\,B,\,\,C,\,\,E\), bán kính của khối cầu này là \(R = IS = \dfrac{1}{2}SC\).

Vì  là hình vuông cạnh  nên \(AC = a\sqrt 2 \).

Áp dụng định lí Pytago trong tam giác vuông  có: \(SC = \sqrt {S{A^2} + A{C^2}}  = \sqrt {2{a^2} + 2{a^2}}  = 2a\).

Vậy \(R = \dfrac{1}{2}SC = a\).