Trong tất cả các hình nón nội tiếp trong hình cầu có thể tích bằng \(36\pi \), bán kính \(r\) của hình nón có diện tích xung quanh lớn nhất là

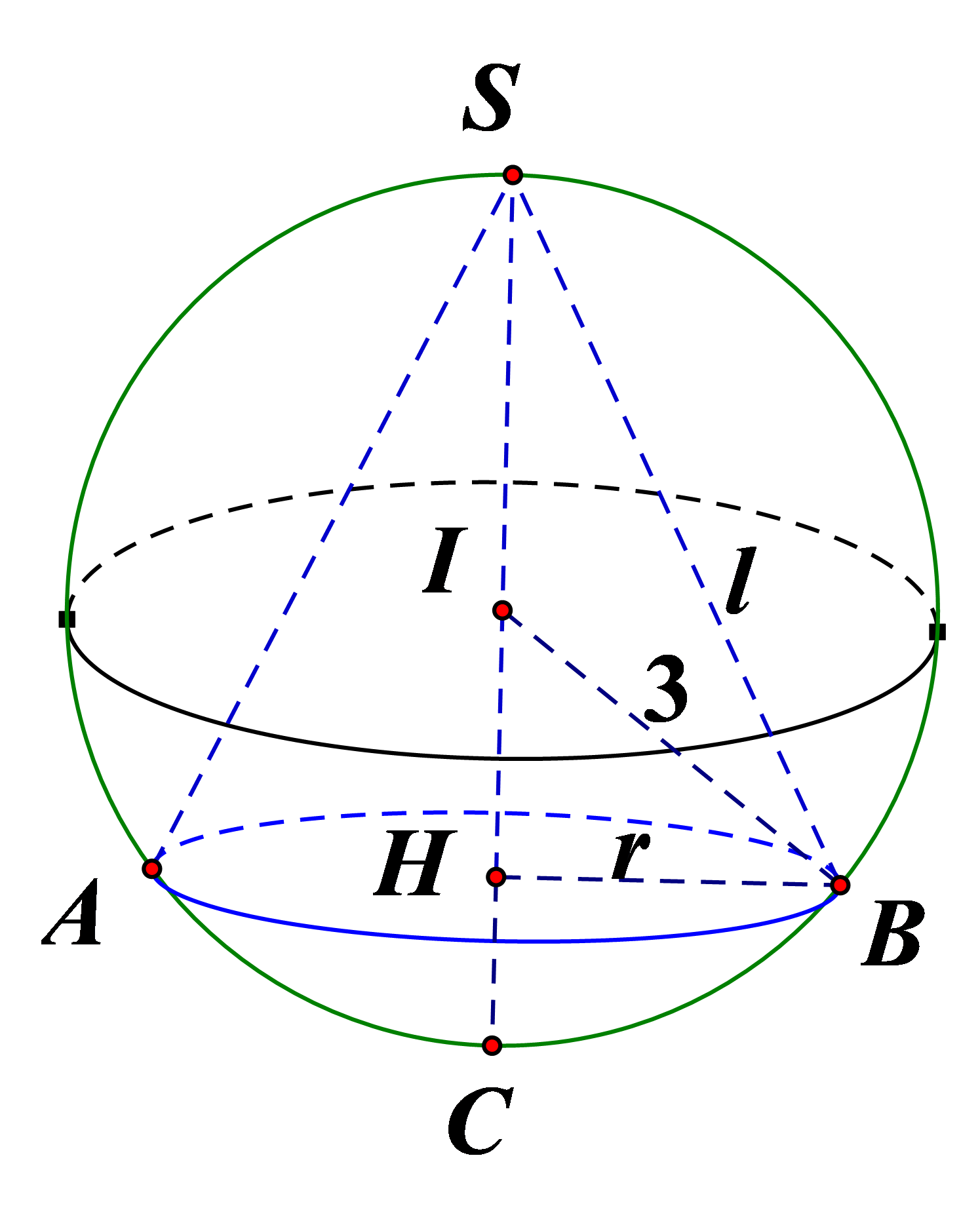
Bước 1: Tính bán kính hình cầu và biểu diễn $r$ và đường sinh $l$ theo chiều cao h của hình nón.

Vì hình cầu có thể tích bằng \(36\pi \) nên bán kính hình cầu là \(R = 3\).

Diện tích xung quanh của hình nón \({S_{xq}} = \pi rl\).

Gọi chiều cao của hình nón là \(h\), khi đó \(h \in (0;6)\).

Ta có \({r^2} = h.(2R - h) = 6h - {h^2}\), suy ra \(r = \sqrt {6h - {h^2}} \).

Lại có \({l^2} = h.2R = 6h\), nên \({S_{xq}} = \pi \sqrt {6h - {h^2}}  \cdot \sqrt {6h}  = \pi \sqrt {36{h^2} - 6{h^3}} \).

Bước 2: Tìm $h$ để diện tích xung quanh lớn nhất, từ đó tìm $r$.

Ta có \(36{h^2} - 6{h^3} = 3{h^2}(12 - 2h)\)\( = 3 \cdot h \cdot h \cdot (12 - 2h) \)\(\le 3 \cdot {\left( {\dfrac{{h + h + 12 - 2h}}{3}} \right)^3}\).

Hay \(36{h^2} - 6{h^3} \le 192\), dấu đẳng thức xảy ra khi \(h = 4\).

Khi đó \(r = \sqrt {6h - {h^2}}  = 2\sqrt 2 \).

Suy ra \({S_{xq}}\) lớn nhất bằng \(8\sqrt 3 \pi \) khi \(r = 2\sqrt 2 \).