Cho hình nón có bán kính đáy \(r = \sqrt 3 ,\) độ dài đường sinh \(l = 4.\) Tính diện tích xung quanh của hình nón đó?
Diện tích xung quanh của hình nón đã cho là: \({S_{xq}} = \pi Rl = \pi .\sqrt 3 .4 = 4\sqrt 3 \pi .\)
Cho hình nón có đường kính đường tròn đáy bằng \(2a,\) chiều cao bằng \(a.\) Khi đó thể tích khối nón bằng:
Bán kính đáy của hình nón là: \(R = 2a:2 = a.\)
Thể tích khối nón đã cho là: \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.a = \dfrac{{\pi {a^3}}}{3}.\)
Cho hình nón có bán kính đáy bằng \(a\). Thiết diện qua trục của hình nón là một tam giác đều. Thể tích khối nón đã cho bằng
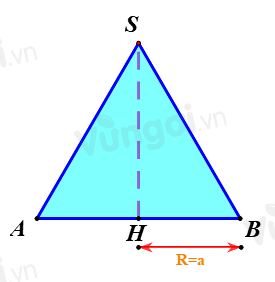
Bước 1: Xác định chiều cao của hình nón.
Ta có: R=a
=> AB=2a
\( \Rightarrow SH = \dfrac{{\sqrt 3 }}{2}.AB = a\sqrt 3 \)
Bước 2: Tính thể tích hình nón
Thể tích hình nón là: \(V = \dfrac{1}{3}.SH.{a^2}\pi = \dfrac{1}{3}.a\sqrt 3 .{a^2}\pi = \dfrac{{{a^3}\pi \sqrt 3 }}{3}\)
Cho hình nón có chiều cao \(h = 4,\) bán kính đáy \(r = 3.\) Diện tích xung quanh của hình nón đã cho bằng:
Diện tích xung quanh của hình nón đã cho là: \({S_{xq}} = \pi Rl = \pi .3.\sqrt {{4^2} + {3^2}} = 15\pi .\)
Đề thi THPT QG 2020 – mã đề 104
Cho khối nón có bán kính đáy \(r = 2\) và chiều cao \(h = 4\). Thể tích của khối nón đã cho bằng
Thể tích khối nón đã cho là: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.2^2}.4 = \dfrac{{16\pi }}{3}.\)
Một đồ chơi bằng gỗ có dạng một khối nón và một nửa khối cầu ghép với nhau (hình bên). Đường sinh của khối nón bằng 5 cm, đường cao của khối nón là 4 cm. Thể tích của đồ chơi bằng:
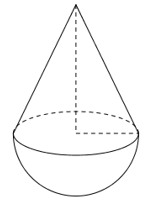
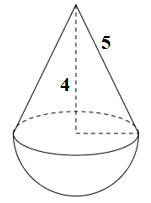
Theo bài ra ta có hình nón có đường sinh \(l = 5\,\,\left( {cm} \right)\), chiều cao \(h = 4\,\,\left( {cm} \right)\). Gọi \(r\) là bán kính đáy hình nón, cũng chính là bán kính hình cầu, ta có \(r = \sqrt {{l^2} - {h^2}} = \sqrt {{5^2} - {4^2}} = 3\,\,\left( {cm} \right)\).
Thể tích khối nón là: \({V_1} = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.3^2}.4 = 12\pi \,\,\left( {c{m^3}} \right)\).
Thể tích nửa khối cầu là: \({V_2} = \dfrac{1}{2}.\dfrac{4}{3}\pi {r^3} = \dfrac{1}{2}.\dfrac{4}{3}\pi {.3^3} = 18\pi \,\,\left( {c{m^3}} \right)\)
Vậy thể tích của đồ chơi bằng: \({V_1} + {V_2} = 12\pi + 18\pi = 30\pi \,\,\left( {c{m^3}} \right)\).
Hình nón \(\left( {\rm N} \right)\) có thiết diện qua trục là tam giác đều có cạnh bằng 4. Diện tích toàn phần của \(\left( {\rm N} \right)\) bằng
Hình nón \(\left( {\rm N} \right)\) có thiết diện qua trục là tam giác đều có cạnh bằng 4 \( \Rightarrow l = 4,\,\,\,r = \dfrac{4}{2} = 2\).
Diện tích toàn phần của hình nón \({S_{tp}} = \pi rl + \pi {r^2} = \pi .2.4 + \pi {.2^2} = 12\pi \).
Đề thi THPT QG 2020 – mã đề 104
Cho hình nón có bán kính đáy bằng 4 và góc ở đỉnh bằng \({60^0}\). Diện tích xung quanh của hình nón đã cho bằng
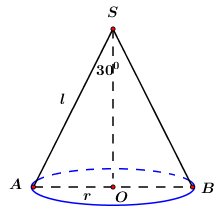
Theo đề bài ta có: \(\widehat {ASB }= {60^0}\) \( \Rightarrow \widehat{ASO} = {30^0}.\)
\( \Rightarrow SA = \dfrac{{OA}}{{\sin \widehat {OSA}}} = \dfrac{4}{{\sin {{30}^0}}} = \dfrac{4}{{\dfrac{1}{2}}} = 8.\)
\( \Rightarrow \) Diện tích xung quanh của hình nón đã cho là: \({S_{xq}} = \pi rl = \pi .4.8 = 32\pi .\)
Đề thi THPT QG - 2021 - mã 102
Cắt hình nón \(\left( \aleph \right)\) bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng \({60^o}\), ta được thiết diện là tam giác đều cạnh \(2a.\) Diện tích xung quanh của \(\left( \aleph \right)\) bằng
Gọi mặt phẳng đi qua đỉnh của hình nón là \(\left( {SAB} \right)\).
Do thiết diện của \(\left( {SAB} \right)\) và hình nón là tam giác đều cạnh \(2a\) nên \(SA = AB = AB = 2a\)
Kẻ \(OH \bot AB\). Nối \(S\) với \(H.\)
Khi đó \(H\) là trung điểm \(AB\) nên \(SH = a\sqrt 3 \)
Ta có: góc giữa \(\left( {SAB} \right)\) và mặt đáy là \(\angle SHO\)
Trong tam giác \(SHO\) vuông tại \(O\) ta có: \(\tan SHO = \dfrac{{SO}}{{OH}}\)\( \Rightarrow \tan {60^o} = \dfrac{{SO}}{{OH}} \Rightarrow SO = \sqrt 3 .OH\)
Theo định lí py-ta-go ta có: \(S{O^2} + O{H^2} = S{H^2}\)\( \Rightarrow 4O{H^2} = S{H^2} \Rightarrow OH = \dfrac{1}{2}SH = \dfrac{{a\sqrt 3 }}{2}\)
\( \Rightarrow SO = \dfrac{{3a}}{2}\)\( \Rightarrow OA = \sqrt {S{A^2} - S{O^2}} = \sqrt {4{a^2} - \dfrac{{9{a^2}}}{4}} = \dfrac{{a\sqrt 7 }}{2}\)
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi .\dfrac{{a\sqrt 7 }}{2}.2a = \pi \sqrt 7 {a^2}\)
Cắt hình nón bởi một mặt phẳng qua trục thu được thiết diện là một tam giác vuông có diện tích bằng 8. Diện tích xung quanh của hình nón đã cho bằng:
Giả sử thiết diện qua trục là tam giác \(SAB\), \(O\) là tâm đường tròn đáy \( \Rightarrow O\) là trung điểm của \(AB\).
Tam giác \(SAB\) vuông tại \(S\) nên \({S_{\Delta SAB}} = \dfrac{1}{2}SA.SB = \dfrac{1}{2}S{A^2} = 8 \Leftrightarrow SA = 4 = l\).
\( \Rightarrow AB = SA\sqrt 2 = 4\sqrt 2 \Rightarrow r = OA = 2\sqrt 2 \).
Vậy diện tích xung quanh hình nón là \({S_{xq}} = \pi rl = \pi .2\sqrt 2 .4 = 8\sqrt 2 \pi \).
Cho hình nón có độ dài đường sinh bằng 5, bán kính bằng 3. Diện tích toàn phần của hình nón bằng:
Diện tích toàn phần của hình nón đã cho là: \({S_{tp}} = \pi Rl + \pi {R^2}\) \( = \pi .3.5 + \pi {.3^2} = 24\pi .\)
Thiết diện qua trục của một khối nón là một tam giác vuông cân và có cạnh góc vuông bằng \(a\sqrt 2 \). Thể tích \(V\) của khối nón bằng:
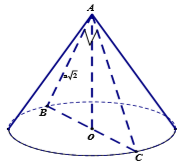
Giả sử thiết diện qua trục là tam giác \(ABC\), theo bài ra ta có \(\Delta ABC\) vuông cân tại \(A\) có \(AB = a\sqrt 2 \).
\( \Rightarrow BC = AB\sqrt 2 = 2a\).
\( \Rightarrow \) Bán kính đáy của hình nón là \(r = \dfrac{1}{2}BC = a\) và chiều cao hình nón là \(h = OA = \dfrac{1}{2}BC = a\).
Vậy thể tích khối nón là \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {a^2}.a = \dfrac{{\pi {a^3}}}{3}\).
Tính diện toàn phần của hình nón có đáy là đường tròn nội tiếp \(\Delta ABD\) và chiều cao bằng chiều cao của lăng trụ.
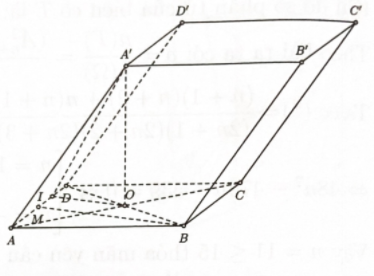
Bước 1: Tính bán kính đường tròn đáy của hình nón.
Vì \(\Delta ABD\) đều nên tâm đường tròn nội tiếp tam giác trùng với trọng tâm của tam giác
\( \Rightarrow \) Bán kính đường tròn đáy của hình nón là: \(r = \dfrac{{BM}}{3} = \dfrac{{a\sqrt 3 }}{6}\).
Bước 2: Tính diện tích xung quanh của hình nón \({S_{xq}} = \pi rl + \pi {r^2}\)
Vì chiều cao của hình nón bằng chiều cao của lăng trụ nên ta có độ dài đường sinh là
\(l = \sqrt {{A^\prime }{O^2} - {r^2}} \)\( = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} - {{\left( {\dfrac{{a\sqrt 3 }}{6}} \right)}^2}} = \dfrac{{a\sqrt {159} }}{6}\)
Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl + \pi {r^2}\)\( = \dfrac{{\pi {a^2}(\sqrt {53} + 1)}}{{12}}\).
Tính thể tích khối tứ diện \(AC{B^\prime }{D^\prime }\).
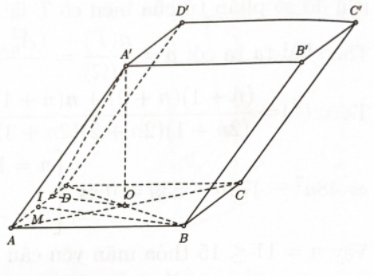
Bước 1: Tính \({S_{ABCD}};A'O\)
Ta có \({S_{ABCD}} = 2{S_{ABD}}\)\( = 2 \cdot \dfrac{1}{2}AB \cdot AD \cdot \sin {60^0 } = \dfrac{{{a^2}\sqrt 3 }}{2};\)\({A^\prime }O = \dfrac{{3a}}{2}\).
Bước 2: Tính \({V_{AC{B^\prime }{D^\prime }}} = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}}\)
=> \({V_{AC{B^\prime }{D^\prime }}} = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}}\)\( = \dfrac{1}{3} \cdot {A^\prime }O \cdot {S_{ABCD}}\)\( = \dfrac{1}{3} \cdot \dfrac{{3a}}{2} \cdot \dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{4}\)
Cho hình nón có độ dài đường sinh bằng \(\dfrac{a}{{\sqrt 2 }}\) và đáy là đường tròn có đường kính bằng \(a,\) diện tích xung quanh của hình nón đó bằng:
Bán kính của đường trón đáy là: \(r = \dfrac{a}{2}.\)
Diện tích xung quanh của hình nón đã cho là: \({S_{xq}} = \pi rl = \pi .\dfrac{a}{2}.\dfrac{a}{{\sqrt 2 }} = \dfrac{{\pi {a^2}\sqrt 2 }}{4}.\)
Tính tan góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\).
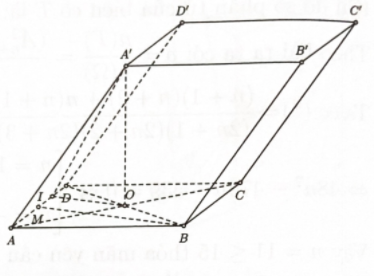
Bước 1: Xác định góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\)
Gọi \(M\) là trung điểm $A D$
\( \Rightarrow BM \bot AD({\mathop{\rm tam}\nolimits} \) giác $A B D$ I$ là trung điểm $M D$
\( \Rightarrow OI \bot AD \Rightarrow \) góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\) bằng \(\widehat {{A^\prime }IO}\).
Bước 2: Tính \(\tan \widehat {{A^\prime }IO}\)
Ta có \(AC = 2AO = 2 \cdot \dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \).
Xét tam giác \(A{A^\prime }O\) vuông tại \(O\) có: \({A^\prime }O = AO \cdot \tan {60^0 } = \dfrac{{a\sqrt 3 }}{2} \cdot \sqrt 3 = \dfrac{{3a}}{2}\).
Xét \(\Delta BMD\) có: \(OI = \dfrac{1}{2}BM = \dfrac{{a\sqrt 3 }}{4}\).
Xét tam giác \({A^\prime }IO\) vuông tại \(O\) có: \(\tan \widehat {{A^\prime }IO} = \dfrac{{{A^\prime }O}}{{OI}} = 2\sqrt 3 \)
Công thức tính diện tích xung quanh hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l\) là
Công thức tính diện tích xung quanh hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l\) là: \({S_{xq}} = \pi rl\)
Diện tích xung quanh hình nón có bán kính đáy \(r = 3cm\) và độ dài đường sinh \(4cm\) là:
Áp dụng công thức \({S_{xq}} = \pi rl\) ta được: \({S_{xq}} = \pi .3.4 = 12\pi \left( {c{m^2}} \right)\)
Cho hình nón bán kính đáy \(r\) và diện tích xung quanh \({S_{xq}}\). Độ dài đường sinh \(l\) của hình nón là:
Từ công thức \({S_{xq}} = \pi rl\) ta có: \(l = \dfrac{{{S_{xq}}}}{{\pi r}}\)
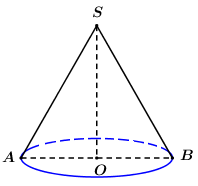
Gọi \(r,l,h\) lần lượt là bán kính đáy, độ dài đường sinh và chiều cao của hình nón. Chọn mệnh đề đúng:
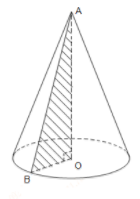
Quan sát hình vẽ ta thấy: \(l = AB,r = OB,h = AO\).
Mà \(A{B^2} = A{O^2} + O{B^2}\) nên \({l^2} = {r^2} + {h^2}\)

