Câu hỏi:
3 năm trước
Thiết diện qua trục của một khối nón là một tam giác vuông cân và có cạnh góc vuông bằng \(a\sqrt 2 \). Thể tích \(V\) của khối nón bằng:
Trả lời bởi giáo viên
Đáp án đúng: b
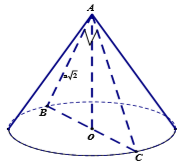
Giả sử thiết diện qua trục là tam giác \(ABC\), theo bài ra ta có \(\Delta ABC\) vuông cân tại \(A\) có \(AB = a\sqrt 2 \).
\( \Rightarrow BC = AB\sqrt 2 = 2a\).
\( \Rightarrow \) Bán kính đáy của hình nón là \(r = \dfrac{1}{2}BC = a\) và chiều cao hình nón là \(h = OA = \dfrac{1}{2}BC = a\).
Vậy thể tích khối nón là \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {a^2}.a = \dfrac{{\pi {a^3}}}{3}\).
Hướng dẫn giải:
- Dựa vào tính chất tam giác vuông cân xác định chiều cao và bán kính đáy của hình nón.
- Khối nón có chiều cao \(h\), bán kính đáy \(r\) có thể tích \(V = \dfrac{1}{3}\pi {r^2}h\).