Câu hỏi:
2 năm trước
Người ta thiết kế một lọ sản phẩm đựng kem chống nắng với thiết kế là một khối cầu như một viên bi khổng lồ, một nửa là nắp hộp, nửa còn lại thiết kế bên trong là một khối trụ nằm nội tiếp nửa mặt cầu để đựng kem chống nắng. Theo dự kiến nhà sản xuất dự định để khối cầu có bán kính \(R = 3\sqrt 2 a\). Để đựng được nhiều kem nhất thì chiều cao của khối trụ là \(h = m\sqrt n a\) với \(m,n \in \mathbb{N}\). Mệnh đề nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: d
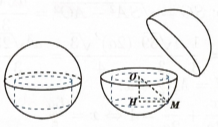
Giả sử chiều cao của khối trụ là \(OH = h(0 \le h \le 3\sqrt 2 a)\).
Ta có \(OM = R = 3\sqrt 2 a,HM = \sqrt {18{a^2} - {h^2}} \).
Vậy \({V_{{\rm{tr }}}} = \pi {\left( {\sqrt {18{a^2} - {h^2}} } \right)^2}.h = \pi \left( {18{a^2} - {h^2}} \right).h\).
Xét hàm số \(y = \pi \left( {18{a^2} - {h^2}} \right)h\) trên đoạn \([0;3\sqrt 2 a]\)
\( \Rightarrow {y^\prime } = \pi \left( {18{a^2} - 3{h^2}} \right)\)
\( \Rightarrow {y^\prime } = 0 \Leftrightarrow h = \sqrt 6 a\).
Ta có \(y(\sqrt 6 a) = 12\sqrt 6 {a^3}\pi ,\)\(y(0) = 0,\)\(y(3\sqrt 2 a) = 0\).
Vậy \({V_{{\rm{tr }}}}\) lớn nhất khi \(h = \sqrt 6 a\)=> m=1; n=6
\( \Rightarrow m + n = 1 + 6 = 7\).
Hướng dẫn giải:
Bước 1: Giả sử chiều cao của khối trụ là \(OH = h(0 \le h \le 3\sqrt 2 a)\).
Tính thể tích của khối trụ theo a và h.
Bước 2: Tìm h để thể tích khối trụ lớn nhất
