Câu hỏi:
3 năm trước
Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật \(ABCD\) có \(AB\) và \(CD\) thuộc hai đáy của hình trụ, \(AB = 4a\),\(AC = 5a\). Thể tích khối trụ là
Trả lời bởi giáo viên
Đáp án đúng: c
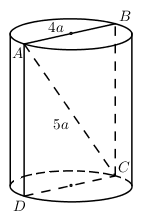
Ta có: \(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {25{a^2} - 16{a^2}} = 3a\) (Định lí Pytago)
Do đó khối trụ có bán kính đáy \(r = \dfrac{{AB}}{2} = 2a\), chiều cao \(h = AC = 3a\).
\( \Rightarrow {V_{tru}} = \pi .{r^2}h = \pi {\left( {2a} \right)^2}.3a = 12\pi {a^3}\).
Hướng dẫn giải:
Sử dụng công thức tính thể tích khối trụ có chiều cao \(h\) và bán kính \(r\) là \(V = \pi {r^2}h\).