Câu hỏi:
2 năm trước
Cắt hình trụ bởi mặt phẳng \(\left( \alpha \right)\) vuông góc với mặt đáy, ta được thiết diện là hình vuông có diện tích bằng 16. Khoảng cách từ tâm đường tròn đáy của hình trụ đến mặt phẳng \(\left( \alpha \right)\) bằng 3. Thể tích khối trụ bằng:
Trả lời bởi giáo viên
Đáp án đúng: b
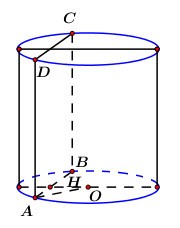
Ta có \(ABCD\) là hình vuông \( \Rightarrow {S_{ABCD}} = A{B^2} = 16\) \( \Rightarrow AB = AD = 4\)
Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB\)
Lại có: \(\left( {ABCD} \right)\) vuông góc với mặt phẳng đáy \( \Rightarrow OH \bot AD\)
\( \Rightarrow OH \bot \left( {ABCD} \right)\) \( \Rightarrow d\left( {O;\,\,\left( {ABCD} \right)} \right) = OH = 3\)
Áp dụng định lý Pitago cho \(\Delta OAH\) vuông tại \(H\) ta có:
\(OA = \sqrt {O{H^2} + {{\left( {\dfrac{{AB}}{2}} \right)}^2}} = \sqrt {{3^2} + {2^2}} = \sqrt {13} \)
Khi đó ta có thể tích của hình trụ đã cho là: \(V = \pi {R^2}h = \pi .O{A^2}.AD = \pi .13.4 = 52\pi .\)
Hướng dẫn giải:
Thể tích khối nón có bán kính đáy \(R\) và đường cao \(h\) là: \(V = \pi {R^2}h.\)
