Khái niệm về mặt tròn xoay (mặt trụ)

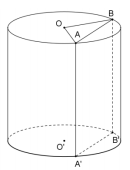
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là $r,\,\,h$.

Theo bài ra ta có: ${S_{xq}} = 4\pi  \Leftrightarrow 2\pi rh = 4\pi  \Leftrightarrow rh = 2$.

Xét tam giác $OAB$ có $OA = OB = r$, $\angle AOB = {120^0}$.

Áp dụng định lí Côsin rong tam giác ta có:

$\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2.OA.OB.\cos \angle AOB\\A{B^2} = {r^2} + {r^2} - 2{r^2}.\dfrac{{ - 1}}{2}\\A{B^2} = 3{r^2}\\ \Rightarrow AB = r\sqrt 3 \end{array}$

$\Rightarrow {S_{ABB'A'}} = AB.BB' = r\sqrt 3 .h = \sqrt 3 rh = 2\sqrt 3$.

Bán kính đường tròn đáy của khối trụ đã cho là: $R = \dfrac{C}{{2\pi }} = \dfrac{{2\pi }}{{2\pi }} = 1.$

$\Rightarrow$ Thể tích của khối trụ đã cho là: $V = \pi {R^2}h = \pi {.1^2}.\sqrt 2  = \sqrt 2 \pi .$

Khi quay hình chữ nhật $ABCD$ quanh cạnh $AB$ ta được khối trụ có chiều cao $h = AB = 4$, bán kính đáy $r = AD = 3$.

Vậy thể tích khối trụ là $V = \pi {r^2}h = \pi {.3^2}.4 = 36\pi$.

Gọi bán kính đáy và chiều cao của hình trụ lần lượt là $r$ và $h\left( {r,h > 0} \right)$

Thiết diện là hình chữ nhật $ABCD$ có chu vi $2\left( {AB + BC} \right) = 2.\left( {h + 2r} \right)$

Theo giả thiết ta có $2\left( {h + 2r} \right) = 12 \Leftrightarrow h + 2r = 6 \Rightarrow h = 6 - 2r\,\,\left( {r < 3} \right)$

Thể tích khối trụ $V = \pi {r^2}h = \pi {r^2}.\left( {6 - 2r} \right) = \pi r.r.\left( {6 - 2r} \right)$

Áp dụng BĐT Cô-si cho 3 số $r;r;6 - 2r$ ta được

$r + r + 6 - 2r \ge 3\sqrt[3]{{r.r\left( {6 - 2r} \right)}} \Leftrightarrow \sqrt[3]{{r.r\left( {6 - 2r} \right)}} \le 2 \Leftrightarrow {r^2}\left( {6 - 2r} \right) \le 8 \Leftrightarrow \pi {r^2}\left( {6 - 2r} \right) \le 8\pi$

Hay $V \le 8\pi$ . Dấu = xảy ra khi $r = 6 - 2r \Leftrightarrow r = 2\left( {TM} \right)$

Vậy giá trị lớn nhất của khối trụ là $V = 8\pi .$ 

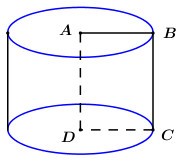
Quay hình chữ nhật ABCD quanh cạnh AD ta được hình trụ có bán kính là $r = AB = a$ và chiều cao là $h = BC = \sqrt {A{C^2} - A{B^2}}  = \sqrt {4{a^2} - {a^2}}  = a\sqrt 3$.

Vây diện tích xung quanh hình trụ:$S = 2\pi rh = 2\pi a.a\sqrt 3  = 2\sqrt 3 \pi {a^2}.$

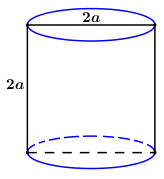
Hình trụ có thiết diện qua trục là hình vuông có cạnh bằng $2a$ nên có chiều cao $h = 2a$ và bán kính đáy $r = a$ . Vậy thể tích khối trụ là $V = \pi {r^2}h = \pi .{a^2}.a = 2\pi {a^3}$.

Ta có $V = \pi {r^2}h \Leftrightarrow 144\pi  = \pi {.6^2}.h \Leftrightarrow h = 4$.

Vậy đường sinh của khối trụ bằng 4.

Ta có: $V = \pi {r^2}h = \pi {.5^2}.3 = 75\pi$

$V = \pi {r^2}h = \pi {.6^2}.3 = 108\pi$.

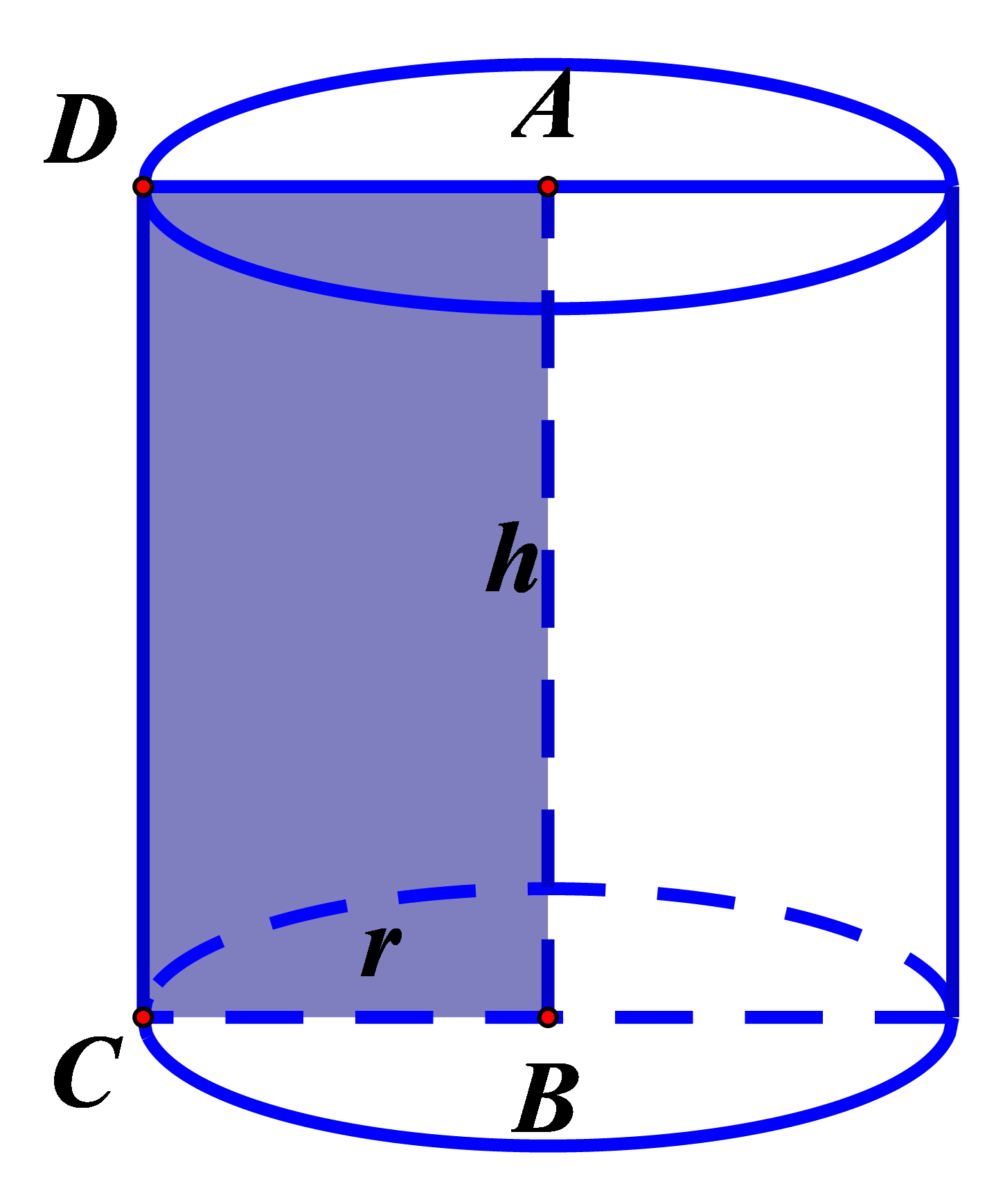
Bước 1: Tính r và h theo a

Vì khối tròn xoay khi quay hình phẳng ABCD quanh trục AB nên độ dài đường cao là độ dài trục:

$h = AB = 2a$.

Bán kính trụ: $r = BC = a$.

Bước 2: Tính V theo a

Thể tích khối trụ là $V = \pi {r^2}h = \pi  \cdot {a^2} \cdot 2a = 2\pi {a^3}$.

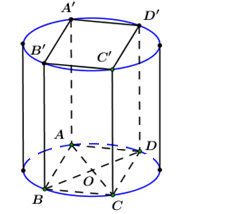
Ta có hình hộp $ABCD.A'B'C'D'$ có các cạnh bằng $a$

$\Rightarrow AA' = a$ là đường sinh của hình trụ.

Bán kính đáy của hình trụ là $R = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}.$

$\Rightarrow$ Diện tích xung quanh của hình trụ là:

${S_{xq}} = 2\pi Rl = 2\pi .\dfrac{{a\sqrt 2 }}{2}.a = \sqrt 2 \pi {a^2}.$  

Diện tích xung quanh của hình trụ đã cho là: ${S_{xq}} = 2\pi rl = 2\pi .7.3 = 42\pi .$

Ta có: $V = \pi {.4^2}.3 = 48\pi$

Ta có: $V = \pi {R^2}h = \pi {.2^2}.3 = 12\pi$.

Công thức tính diện tích xung quanh hình trụ: ${S_{xq}} = 2\pi rh$.

Ta có: ${S_{xq}} = 2\pi rh = 2\pi .2.5 = 20\pi c{m^2}$

Công thức tính diện tích toàn phần hình trụ là: ${S_{tp}} = 2\pi rh + 2\pi {r^2}$.

Ta có: ${S_{tp}} = {S_{xq}} + 2{S_d} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {h + r} \right) = {C_d}.\left( {h + r} \right)$

Dó đó công thức ở đáp án D là sai.

Ta có: ${S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi .5.3 + 2\pi {.5^2} \approx 251,3c{m^2}$

Công thức tính thể tích khối trụ là $V = \pi {r^2}h$