Câu hỏi:
2 năm trước
Cho hình trụ có đáy là hai đường tròn tâm \(O\) và \({O^\prime }\), bán kính đáy bằng chiều cao và bằng 2 a. Trên đường tròn đáy có tâm \(O\) lấy điểm \(A\), trên đường tròn tâm \({O^\prime }\) lấy điểm \(B\). Đặt \(\alpha \) là góc giữa AB và đáy. Tính \(\tan \alpha \) khi thể tích khối tứ diện \(O{O^\prime }AB\) đạt giá trị lớn nhất.
Trả lời bởi giáo viên
Đáp án đúng: b
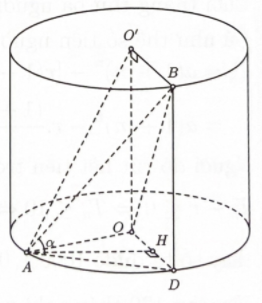
Gọi \(D\) là hình chiếu vuông góc của \(B\) lên mặt phẳng \((O)\).
Kẻ \(AH \bot OD,H \in OD\).
Ta có thể tích của khối chóp \(OO'AB\) là
\({V_{OO'AB}} = \dfrac{1}{3}AH \cdot {S_{\Delta OO'B}} = \dfrac{{2{a^2}}}{3} \cdot AH\)\( \le \dfrac{{2{a^2}}}{3} \cdot AO = \dfrac{{4{a^3}}}{3}\)
\({\left( {{V_{OO'AB}}} \right)_{\max }} \Leftrightarrow H \equiv O\).
Suy ra \(AD = 2\sqrt 2 a\).
Vậy \(\tan \alpha = \tan \widehat {BAD} = \dfrac{1}{{\sqrt 2 }}\).
Hướng dẫn giải:
- Gọi \(D\) là hình chiếu vuông góc của \(B\) lên mặt phẳng \((O)\). Kẻ \(AH \bot OD,H \in OD\).
- Tính \({\left( {{V_{OO'AB}}} \right)_{\max }}\) (theo a) rồi vị trí của H.
- Tính \(\tan \alpha \)
