Câu hỏi:
2 năm trước
Cho hình trụ có chiều cao bằng $6\sqrt 2 \,\,cm.$ Biết rằng một mặt phẳng không vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song$AB,\,\,CD$ mà $AB = CD = 6\,\,cm,$ diện tích tứ giác $ABCD$ bằng $60\,\,c{m^2}.$ Tính bán kính đáy của hình trụ.
Trả lời bởi giáo viên
Đáp án đúng: d
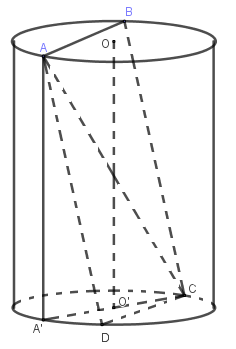
Vì $AB = CD;\,\,AB$//$CD$$ \Rightarrow \,\,ABCD$ là hình chữ nhật $ \Rightarrow \,\,AD = 10\,\,cm.$
Xét hình chữ nhật \(ABCD\) có \(AD\) không song song và không vuông góc với trục \(OO'\) của hình trụ.
Dựng đường sinh $AA'$, ta có \(\left\{ \begin{array}{l}CD \bot AA'\\CD \bot AD\end{array} \right. \Rightarrow CD \bot \left( {AA'D} \right) \Rightarrow CD \bot A'D\)
Suy ra \(A'C\) là đường kính đáy nên \(A'C = 2R\)
Xét tam giác vuông \(AA'C,\) có \(A'C = \sqrt {A{C^2} - A{{A'}^2}} = \sqrt {{{\left( {2\sqrt {34} } \right)}^2} - {{\left( {6\sqrt 2 } \right)}^2}} = 8.\)
Suy ra độ dài bán kính đáy của hình trụ là \(2R = 8 \Leftrightarrow R = 4\,\,cm.\)
Hướng dẫn giải:
Vẽ hình, xác định các yếu tố liên quan đến đường sinh, bán kính đáy
