Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với đáy và \(SA = a\sqrt 2 ;\,\widehat {BAC} = {45^0}\). Biết bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\) bằng \(a\). Tính độ dài cạnh \(BC\).
Trả lời bởi giáo viên
Đáp án đúng: a
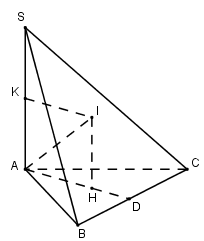
Gọi \(H\) là tâm đường tròn ngoại tiếp tam giác \(ABC\), qua \(H\) kẻ đường thẳng \(d//SA \Rightarrow d \bot \left( {ABC} \right)\)
Gọi \(K\) là trung điểm của \(SA\), qua \(K\) kẻ đường thẳng song song với \(AH\) cắt \(d\) tại \(I\)
\( \Rightarrow I\) là tăm mặt cầu ngoại tiếp tam giác \(ABC\)
Xét tam giác vuông \(AHI\) có
\(AH = \sqrt {A{I^2} - I{H^2}} = \sqrt {A{I^2} - {{\left( {\dfrac{{SA}}{2}} \right)}^2}} = \dfrac{a}{{\sqrt 2 }} = R\)
Ta có
\(\begin{array}{l}{S_{\Delta ABC}} = \dfrac{1}{2}AB.AC.\sin {45^0} = \dfrac{{AB.AC.BC}}{{4R}}\\ \Rightarrow BC = 2R.\sin {45^0} = \dfrac{{2a}}{{\sqrt 2 }}.\dfrac{1}{{\sqrt 2 }} = a\end{array}\)
Hướng dẫn giải:
Dựng tâm đường tròn ngoại tiếp \(H\) tam giác \(ABC\), dựng tâm \(I\) của đường tròn ngoại tiếp chóp \(S.ABC\)
Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\).
Sử dụng các công thức tính diện tích tam giác \({S_{\Delta ABC}} = \dfrac{1}{2}.AB.AC.\sin \widehat {BAC} = \dfrac{{AB.AC.BC}}{{4R}}\)
