Cho hình nón tròn xoay đỉnh $S,$ đáy là hình tròn tâm $O.$ Trên đường tròn đó lấy hai điểm $A$ và $M. $ Biết góc $\widehat {AOM} = {60^0}$, góc tạo bởi hai mặt phẳng $(SAM)$ và $(OAM)$ có số đo bằng ${30^0}$ và khoảng cách từ $O$ đến $(SAM)$ bằng $2.$ Khi đó thể tích khối nón là:
Trả lời bởi giáo viên
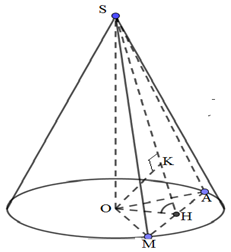
Kẻ $OH\bot AM,\,\,H\in AM,\,\,\,\,\,OK\bot SH,\,\,K\in SH$
Vì $\left\{ \begin{align}& AM\bot SO \\ & AM\bot OH \\\end{align} \right.\Rightarrow AM\bot (SOH)\Rightarrow AM\bot OK$
Mà $OK \bot SH \Rightarrow OK \bot (SAM) \Rightarrow d(O,(SAM)) = OK = 2$
Ta có: $\left\{ \begin{array}{l}(SAM) \cap (OAM) = AM\\AM \bot (SOH)\end{array} \right.$ (vì $AM \bot OH,\,\,AM \bot SO$)
Mà $(SOH) \cap (OAM) = OH,\,\,(SOH) \cap (SAM) = SH$
$ \Rightarrow \left( {\widehat {(SAM),(OAM)}} \right) = \left( {\widehat {SH,OH}} \right) = \widehat {SHO} = {30^0}$
Tam giác OHK vuông tại K $ \Rightarrow OH = \dfrac{{OK}}{{\sin \widehat H}} = \dfrac{2}{{\sin {{30}^0}}} = 4$
Tam giác SOH vuông tại O $ \Rightarrow SO = OH.\tan \widehat H = 4.\tan {30^0} = \dfrac{4}{{\sqrt 3 }}$
Tam giác OAM cân tại O, $\widehat {AOM} = {60^0}$, $OH \bot AM \Rightarrow \widehat {HOM} = \dfrac{{\widehat {AOM}}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}$
Tam giác OHM vuông tại H $ \Rightarrow OM = \dfrac{{OH}}{{\cos \widehat {HOM}}} = \dfrac{4}{{\cos {{30}^0}}} = \dfrac{4}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{8}{{\sqrt 3 }}$
Thể tích khối nón: $V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .O{M^2}.SO = \dfrac{1}{3}\pi {\left( {\dfrac{8}{{\sqrt 3 }}} \right)^2}.\dfrac{4}{{\sqrt 3 }} = \dfrac{{256\sqrt 3 \pi }}{{27}}$
Hướng dẫn giải:
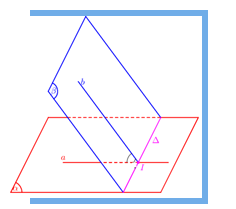
Xác định góc giữa hai mặt phẳng $\left( \alpha \right),\,\,\left( \beta \right)$:
- Tìm giao tuyến $\Delta $ của $\left( \alpha \right),\,\,\left( \beta \right)$.
- Xác định 1 mặt phẳng $\left( \gamma \right) \bot \Delta $.
- Tìm các giao tuyến $a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right)$
- Góc giữa hai mặt phẳng $\left( \alpha \right),\,\,\left( \beta \right)$: $\left( {\widehat {\left( \alpha \right);\left( \beta \right)}} \right) = \left( {\widehat {a;b}} \right)$