Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông cân tại \(A\) có \(AB = AC = 12\). Lấy một điểm \(M\) thuộc cạnh huyền \(BC\) và gọi \(H\) là hình chiếu của \(M\) lên cạnh góc vuông \(AB\). Quay tam giác \(AMH\) quanh trục là đường thẳng \(AB\) tạo thành mặt nón tròn xoay \(\left( N \right)\), hỏi thế tích \(V\) của khối nón tròn xoay \(\left( N \right)\) lớn nhất là bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: c
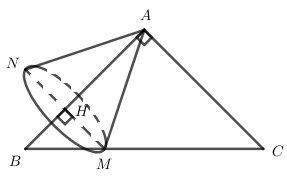
Quay tam giác vuông \(AMH\) quanh trục \(AB\) ta được khối nón có đỉnh \(A\), bán kính đát \(HM\) và đường cao \(AH\) , khi đó ta có thể tích của khối nón tròn xoay \(\left( N \right)\) là \(V = \dfrac{1}{3}\pi H{M^2}.AH\)
Đặt \(HM = x,\,\,\left( {0 \le x \le 12\sqrt 2 } \right)\) ta có \(\Delta BHM\) vuông cân tại \(H\) nên \(BH = HM = x \Rightarrow AH = AB - BH = 12 - x\)
Khi đó \(V = \dfrac{1}{3}\pi {x^2}\left( {12 - x} \right)\)
Xét hàm số \(f\left( x \right) = {x^2}\left( {12 - x} \right)\) với \(x \in \left[ {0;12\sqrt 2 } \right]\)
\(\begin{array}{l}f'\left( x \right) = 2x\left( {12 - x} \right) - {x^2} = - 3{x^2} + 24x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 8\end{array} \right.\\\left\{ \begin{array}{l}f\left( 0 \right) = 0\\f\left( {12} \right) = 0\\f\left( 8 \right) = 256\end{array} \right. \Rightarrow \mathop {\max }\limits_{\left[ {0;12\sqrt 2 } \right]} f\left( x \right) = 256\\ \Rightarrow {V_{max}} = \dfrac{1}{3}\pi .256 = \dfrac{{256\pi }}{3}\end{array}\)
Hướng dẫn giải:
Đặt \(HM = x\), lập hàm thể tích khối nón \(\left( N \right)\) và tìm GTLN của hàm số đó.
