Câu hỏi:
2 năm trước
Tứ diện \(ABCD\) có \(AB = 2,CD = 2\sqrt 2 ,\widehat {ABC} = \widehat {DAB} = {90^0}\) và góc giữa \(AD,BC\) bằng \({45^0}\). Khi đó, bán kính mặt cầu ngoại tiếp tứ diện là:
Trả lời bởi giáo viên
Đáp án đúng: b
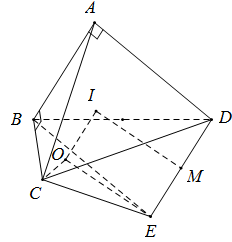
Dựng hình chữ nhật ABED. Ta có mặt cầu tâm I ngoại tiếp tứ diện ABCD cũng phải đi qua điểm E
Do đó I là tâm mặt cầu ngoại tiếp tứ diện BCDE
Ta có AB ⊥ BE; AB ⊥ BC ⇒ AB ⊥ (BCE)
Vì DE // AB nên DE ⊥ (BCE)
Dựng tam giác vuông cân COE trong mặt phẳng (BCE) sao cho B và O nằm cùng phía với CE
Ta chứng minh được O là tâm đường tròn ngoại tiếp ∆ BCE. Dựng hình chữ nhật MEOI với M là trung điểm DE thì I là giao của mặt phẳng trung trực của DE với trục của đường tròn ngoại tiếp ∆ BCE nên I là tâm mặt cầu ngoại tiếp tứ diện $BCDE$
Ta có: $ME = \dfrac{{DE}}{2} = \dfrac{{AB}}{2} = 1$
$OE = \dfrac{{CE}}{{\sqrt 2 }} = \dfrac{{\sqrt {C{D^2} - D{E^2}} }}{{\sqrt 2 }} = \dfrac{{\sqrt {C{D^2} - A{B^2}} }}{{\sqrt 2 }} = \sqrt 2 \Rightarrow IM = OE = \sqrt 2 $ (vì ∆ CED vuông tại E)
$ \Rightarrow R = IE = \sqrt {I{M^2} + M{E^2}} = \sqrt 3 $
Hướng dẫn giải:
- Dựng hình chữ nhật $ABED.$ Ta có mặt cầu tâm $I$ ngoại tiếp tứ diện $ABCD$ cũng phải đi qua điểm $E$.
- Dựng tâm và tính bán kính mặt cầu đi qua các điểm \(A,B,C,D,E\).
