Đồ thị sau đây là của hàm số nào ?

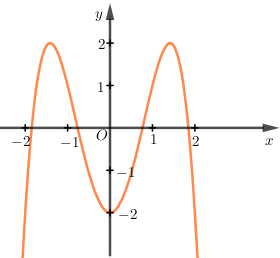
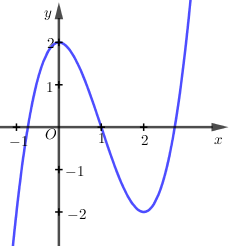
Dựa vào hình vẽ, ta thấy rằng :

Hàm số là hàm số trùng phương, có dạng $y = a{x^4} + b{x^2} + C.$

 Giới hạn $\mathop {\lim }\limits_{x{\kern 1pt}  \to {\kern 1pt}  + {\kern 1pt} \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x{\kern 1pt}  \to {\kern 1pt}  - \infty } {\mkern 1mu} y =  - {\mkern 1mu} \infty $$ \Rightarrow $ Hệ số $a < 0.$

 Đồ thị hàm số cắt trục Oy tại $\left( {0; - {\mkern 1mu} 2} \right)$$ \Rightarrow $$c =  - {\mkern 1mu} 2.$

 Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt. Hàm số có ba điểm cực trị, trong đó có điểm cực trị có hoành độ lớn hơn 1.

Vậy hàm số cần tìm là $y =  - {\mkern 1mu} {x^4} + 4{x^2} - 2.$