Trong không gian với hệ tọa độ \(Oxyz\), cho \(A\left( {2; - 1;3} \right)\), \(B\left( {4;0;1} \right)\), \(C\left( { - 10;5;3} \right)\). Độ dài đường phân giác trong góc \(\widehat B\) của tam giác \(ABC\) bằng:
Gọi \(D\) là chân phân giác trong của góc \(\widehat B\), ta có \(\dfrac{{DA}}{{DC}} = \dfrac{{BA}}{{BC}} = \dfrac{3}{{15}} \Rightarrow \overrightarrow {DA} = - \dfrac{1}{5}\overrightarrow {DC} \)
Gọi \(D\left( {x;y;z} \right)\) ta có: \(\overrightarrow {DA} = - \dfrac{1}{5}\overrightarrow {DC} \Leftrightarrow - 5\overrightarrow {DA} = \overrightarrow {DC} \)\( \Leftrightarrow \left\{ \begin{array}{l} - 5\left( {2 - x} \right) = - 10 - x\\ - 5\left( { - 1 - y} \right) = 5 - y\\ - 5\left( {3 - z} \right) = 3 - z\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}6x = 0\\6y = 0\\6z = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 0\\z = 3\end{array} \right.\)
Suy ra \(D\left( {0;0;3} \right)\). Vậy \(BD = 2\sqrt 5 \).
Trong không gian với hệ tọa độ \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {0; - 4;0} \right)\), \(B\left( { - 5;6;0} \right)\), \(C\left( {3;2;0} \right)\). Tọa độ chân đường phân giác ngoài góc \(\widehat A\) của tam giác \(ABC\) là:
Gọi \(F\) là chân đường phân giác ngoài góc \(\widehat A\) của tam giác \(ABC\), ta có \(\overrightarrow {FB} = \dfrac{{AB}}{{AC}}.\overrightarrow {FC} \).
Tính được \(AB = 5\sqrt 5 \,\,,\,\,AC = 3\sqrt 5 \). Suy ra $\overrightarrow {FB} = \dfrac{5}{3}\overrightarrow {FC} \Leftrightarrow 3\overrightarrow {FB} = 5\overrightarrow {FC} $.
Gọi \(F\left( {x;y;z} \right)\). Từ \(3\overrightarrow {FB} = 5\overrightarrow {FC} \Rightarrow \left\{ \begin{array}{l}3\left( { - 5 - x} \right) = 5\left( {3 - x} \right)\\3\left( {6 - y} \right) = 5\left( {2 - y} \right)\\3\left( {0 - z} \right) = 5\left( {0 - z} \right)\end{array} \right.\, \Rightarrow \left\{ \begin{array}{l}x = 15\\y = - 4\\z = 0\end{array} \right.\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {1;1; - 6} \right)\), \(B\left( {0;0; - 2} \right)\), \(C\left( { - 5;1;2} \right)\) và \(D'\left( {2;1; - 1} \right)\). Thể tích của khối hộp đã cho bằng:
Do \(ABCD.A'B'C'D'\) là hình hộp nên ta có $\overrightarrow {A'D'} = \overrightarrow {BC} $, suy ra $A'\left( {7;0; - 5} \right)$.
Và $\overrightarrow {AA'} = \overrightarrow {BB'} $ nên suy ra $B'\left( {6; - 1; - 1} \right)$.
Ta có \(\overrightarrow {BA} = \left( {1;1; - 4} \right)\), \(\overrightarrow {BC} = \left( { - 5;1;4} \right)\) và \(\overrightarrow {BB'} = \left( {6; - 1;1} \right)\)
Thể tích khối hộp \({V_{ABCD.A'B'C'D'}} = \left| {\left[ {\overrightarrow {BB'} ,\overrightarrow {BC} } \right].\overrightarrow {BA} } \right| = 38\)
Trong không gian với hệ tọa độ \(Oxyz\), cho tứ diện \(ABCD\) với \(A\left( { - 1; - 2;4} \right)\), \(B\left( { - 4; - 2;0} \right)\), \(C\left( {3; - 2;1} \right)\) và \(D\left( {1;1;1} \right)\). Độ dài đường cao của tứ diện \(ABCD\) kẻ từ đỉnh \(D\) bằng:
Ta có: \(\overrightarrow {AB} = \left( { - 3;0; - 4} \right),\overrightarrow {AC} = \left( {4;0; - 3} \right),\) \(\overrightarrow {AD} = \left( {2;3; - 3} \right)\) nên \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0; - 25;0} \right)\)
Diện tích tam giác ${S_{\Delta ABC}} = \dfrac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right| = \dfrac{{25}}{2}$
Thể tích tứ diện \({V_{ABCD}} = \dfrac{1}{6}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right| = \dfrac{{25}}{2}\).
Suy ra độ dài đường cao \(h = d\left( {D,\left( {ABC} \right)} \right) = \dfrac{{3{V_{ABCD}}}}{{{S_{\Delta ABC}}}} = 3\).
Trong không gian $Oxyz$, cho \(\vec a = (1;2;1),\vec b = ( - 1;1;2),\vec c = (x;3x;x + 2)\). Nếu 3 vectơ \(\vec a,\vec b,\vec c\) đồng phẳng thì \(x\) bằng
Bước 1: Tính \(\left[ {\overrightarrow a ;\overrightarrow b } \right]\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\vec a = (1;2;1)}\\{\vec b = ( - 1;1;2)}\end{array} \Rightarrow [\vec a;\vec b] = (3; - 3;3)} \right.\).
Bước 2: Tìm x
Khi đó \(\vec c,\vec b,\vec c\) đồng phẳng \( \Leftrightarrow [\vec a;\vec b] \cdot \vec c = 0\)\( \Leftrightarrow 3x - 9x + 3\left( {x + 2} \right) = 0 \Leftrightarrow x = 2\)
Trong không gian Oxyz, cho các điểm \(A\left( 2;-2;\ 1 \right),\ B\left( 1;-1;\ 3 \right).\) Tọa độ của vecto \(\overrightarrow{AB}\) là
Ta có: \(\overrightarrow{AB}=\left( {{x}_{2}}-{{x}_{1}};{{y}_{2}}-{{y}_{1}};\ {{z}_{2}}-{{z}_{1}} \right)=\left( 1-2;\ -1+2;\ 3-1 \right)=\left( -1;\ 1;\ 2 \right).\)
Trong không gian với hệ tọa độ \(Oxyz,\) cho hai điểm \(A\left( 3;-\,4;0 \right),\,\,B\left( 0;2;4 \right).\) Tọa độ \(\overrightarrow{AB}\) là
Ta có \(A\left( 3;-\,4;0 \right),\,\,B\left( 0;2;4 \right)\,\,\Rightarrow \,\,\overrightarrow{AB}=\left( -\,3;6;4 \right).\)
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;0;5} \right)\) và \(B\left( {7;9;0} \right)\). Điểm \(M\) di động trên tia \(Oz\), điểm \(N\) di động trên tia \(Oy\). Đường gấp khúc \(AMNB\) có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục)
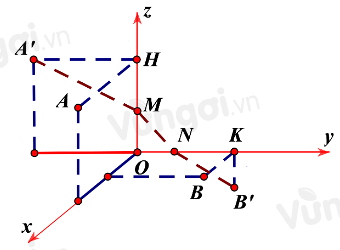
Trục \(Oz\) đi qua điểm \(O\left( {0;0;0} \right)\) và có vectơ chỉ phương \(\vec k\left( {0;0;1} \right)\).
Suy ra phương trình trục \(Oz\) là: \(\left\{ \begin{array}{l}x = 0\\y = 0\\z = t\end{array} \right.\).
Gọi \(\left( \alpha \right)\) là mặt phẳng chứa điểm \(A\) và vuông góc với trục \(Oz\).
Suy ra \(\left( \alpha \right)\) nhận \(\vec k\left( {0;0;1} \right)\) làm vectơ pháp tuyến.
Mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {1;0;5} \right)\) và có vectơ pháp tuyến \(\vec k\left( {0;0;1} \right)\).
Suy ra phương trình mặt phẳng \(\left( \alpha \right)\): \(0.\left( {x - 1} \right) + 0.\left( {y - 0} \right) + 1.\left( {z - 5} \right) = 0\)
\( \Leftrightarrow z - 5 = 0\).
Gọi \(H\) là giao điểm của trục \(Oz\) và mặt phẳng \(\left( \alpha \right)\).
Ta có \(H \in Oz \Rightarrow H\left( {0;0;t} \right)\).
Lại có \(H \in \left( \alpha \right) \Rightarrow t = 5\).
Khi đó \(H\left( {0;0;5} \right)\).
Chứng minh tương tự, ta tìm được hình chiếu của điểm \(B\) lên trục \(Oy\) là \(K\left( {0;9;0} \right)\).
Chọn \(A'\left( {0; - 1;5} \right) \in \left( {Oyz} \right)\) và \(B'\left( {0;9; - 7} \right) \in \left( {Oyz} \right)\).
Suy ra \(\overrightarrow {A'B'} = \left( {0;10; - 12} \right) \Rightarrow A'B' = 2\sqrt {61} \).
Xét \(\Delta AHM\) và \(\Delta A'HM\), có:
\(HM\) chung.
\(AH = A'H\,\,\left( { = 1} \right)\).
\(\widehat {AHM} = \widehat {A'HM} = 90^\circ \).
Do đó \(\Delta AHM = \Delta A'HM\) (c.g.c)
\( \Rightarrow AM = A'M\) (cặp cạnh tương ứng)
Chứng minh tương tự, ta được \(BN = B'N\).
Trong mặt phẳng \(\left( {Oyz} \right)\), ta có độ dài đường gấp khúc \(AMNB\) là:
\(AM + MN + NB = A'M + MN + NB' \ge A'B' = 2\sqrt {61} \).
Khi đó độ dài nhỏ nhất của đường gấp khúc \(AMNB\) là \(2\sqrt {61} \approx 15,6\).
Vậy ta chọn phương án B.
Trong không gian với hệ tọa độ $Oxyz$ , cho điểm $M$ thỏa mãn hệ thức \(\overrightarrow {OM} = 2\vec i + \vec j\). Tọa độ của điểm $M$ là
Ta có: \(\overrightarrow {OM} = 2\vec i + \vec j \Rightarrow \overrightarrow {OM} = 2.\vec i + 1.\vec j + 0.\overrightarrow k \Leftrightarrow M\left( {2;1;0} \right)\)
Trong không gian với hệ tọa độ $Oxyz$, cho \(\overrightarrow {OM} = 2\vec j - \vec k\) và \(\overrightarrow {ON} = 2\vec j - 3\vec i\). Tọa độ của \(\overrightarrow {MN} \) là:
Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = \left( {2\vec j - 3\vec i} \right) - \left( {2\vec j - \vec k} \right) = - 3\vec i + \vec k\)
Suy ra $\overrightarrow {MN} = \left( { - 3;0;1} \right)$.
Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( {0; - 2;3} \right),B\left( {1;0; - 1} \right)$. Gọi $M$ là trung điểm đoạn $AB$. Khẳng định nào sau đây là đúng?
Ta có: \(\overrightarrow {BA} = (0 - 1; - 2 - 0;3 + 1) = ( - 1; - 2;4)\). Suy ra A sai.
Suy ra \(\overrightarrow {AB} = (1;2; - 4)\), D sai.
Có \(AB = \sqrt {{1^2} + {2^2} + {{( - 4)}^2}} = \sqrt {21} \). B đúng.
Mà \(M\) là trung điểm của \(AB\) nên \(M\left( {\frac{1}{2}; - 1;1} \right)\), C sai.
Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $M\left( {2; - 3;5} \right),N\left( {6; - 4; - 1} \right)$ và đặt \(u = \left| {\overrightarrow {MN} } \right|\). Mệnh đề nào sau đây là mệnh đề đúng?
Ta có \(\overrightarrow {MN} = (6 - 2; - 4 + 3; - 1 - 5) = (4; - 1; - 6)\).
Do đó\(|\overrightarrow {MN} | = \sqrt {{4^2} + {{( - 1)}^2} + {{( - 6)}^2}} = \sqrt {53} \)
Trong không gian $Oxyz$ cho ba vecto \(\vec a = \left( { - 1;1;0} \right),\vec b = \left( {1;1;0} \right),\vec c = \left( {1;1;1} \right)\). Mệnh đề nào dưới đây sai?
Kiểm tra lần lượt các điều kiện
\(\left\{ \begin{array}{l}\left| {\vec a} \right| = \sqrt {{{( - 1)}^2} + {1^2} + {0^2}} = \sqrt 2 \\\left| {\vec c} \right| = \sqrt {{1^2} + {1^2} + {1^2}} = \sqrt 3 \\\vec a.\vec b = ( - 1).1 + 1.1 + 0.0 = 0 \Rightarrow \vec a \bot \vec b\end{array} \right.\)
Lại có: \(\overrightarrow b .\overrightarrow c = 1.1 + 1.1 + 0.1 = 2 \ne 0\) nên \(\overrightarrow b \) và \(\overrightarrow c \) không vuông góc.
Trong không gian $Oxyz$ cho $3$ véc tơ: \(\vec a\left( {4;2;5} \right),\vec b\left( {3;1;3} \right),\vec c\left( {2;0;1} \right)\). Kết luận nào sau đây đúng
Tính \(\left[ {\vec a,\vec b} \right] = \left( {\left| {\begin{array}{*{20}{c}}2&5\\1&3\end{array}} \right|;\left| {\begin{array}{*{20}{c}}5&4\\3&3\end{array}} \right|;\left| {\begin{array}{*{20}{c}}4&2\\3&1\end{array}} \right|} \right) = \left( {1;3; - 2} \right)\). Suy ra loại A
Tính \(\left[ {\vec a,\vec b} \right].\vec c = \left( {1;3; - 2} \right).\left( {2;0;1} \right) = 0\). Suy ra \(\vec a,\vec b,\vec c\) đồng phẳng.
Cho tam giác $ABC$ biết $A\left( {2;4; - 3} \right)$ và trọng tâm $G$ của tam giác có toạ độ là $G\left( {2;1;0} \right)$. Khi đó \(\overrightarrow {AB} + \overrightarrow {AC} \) có tọa độ là
Gọi $M$ là trung điểm của $BC$. Ta có \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \).
Do tính chất trọng tâm có \(\overrightarrow {AM} = \dfrac{3}{2}\overrightarrow {AG} \). Suy ra\(\overrightarrow {AB} + \overrightarrow {AC} = 3\overrightarrow {AG} \).
Mà \(\overrightarrow {AG} = \left( {2 - 2;1 - 4;0 - ( - 3)} \right) = \left( {0; - 3;3} \right)\). Suy ra \(3\overrightarrow {AG} = (0; - 9;9)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 2\sqrt 3 ,{\rm{ }}\left| {\overrightarrow b } \right| = 3\) và $\left( {\overrightarrow a ,\overrightarrow b } \right) = {30^0}$. Độ dài của vectơ \(\left[ {5\overrightarrow a , - 2\overrightarrow b } \right]\) bằng:
Chú ý rằng \(\left( {5\overrightarrow a , - 2\overrightarrow b } \right) = {180^0} - \left( {\overrightarrow a ,\overrightarrow b } \right) = {150^0}.\)
Sử dụng công thức \(\left| {\left[ {m\vec a,n\vec b} \right]} \right| = \left| {m.n} \right|.\left| {\vec a} \right|.\left| {\vec b} \right|.\sin \left( {m\vec a,n\vec b} \right)\), ta được
\(\left| {\left[ {5\overrightarrow a , - 2\overrightarrow b } \right]} \right| = \left| {5.\left( { - 2} \right)} \right|.2\sqrt 3 .3.\sin {150^0} = 30\sqrt 3 .\)
Trong không gian với hệ trục tọa độ $Oxyz$, cho ba điểm $A\left( {1;2; - 1} \right),B\left( {2; - 1;3} \right),C\left( { - 3;5;1} \right)$. Tìm tọa độ điểm $D$ sao cho tứ giác $ABCD$ là hình bình hành.
Có \(\overrightarrow {AB} = \left( {2 - 1; - 1 - 2;3 + 1} \right) = \left( {1; - 3;4} \right)\) và \(\overrightarrow {DC} = ( - 3 - {x_D};5 - {y_D};1 - {z_D})\).
ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l} - 3 - {x_D} = 1\\5 - {y_D} = - 3\\1 - {z_D} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = - 4\\{y_D} = 8\\{z_D} = - 3\end{array} \right.\)
Cho hình bình hành $ABCD$ với $A\left( {2;4; - 4} \right),B\left( {1;1; - 3} \right),C\left( { - 2;0;5} \right),D\left( { - 1;3;4} \right)$. Diện tích của hình bình hành $ABCD$ bằng
Có \(\overrightarrow {AB} = \left( {1 - 2;1 - 4; - 3 + 4} \right) = \left( { - 1; - 3;1} \right)\) và \(\overrightarrow {AC} = \left( { - 2 - 2;0 - 4;5 + 4} \right) = \left( { - 4; - 4;9} \right)\).
Tính \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 3}&1\\{ - 4}&9\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&{ - 1}\\9&{ - 4}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 3}\\{ - 4}&{ - 4}\end{array}} \right|} \right) = \left( { - 23;5; - 8} \right)\).
Áp dụng công thức tính diện tích hình bình hành có
\({S_{ABCD}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right| = \sqrt {{{( - 23)}^2} + {5^2} + {{( - 8)}^2}} = \sqrt {618} \)
Trong không gian với hệ tọa độ $Oxyz$, các điểm $A\left( {1;2;3} \right),B\left( {3;3;4} \right),C\left( { - 1;1;2} \right)$ sẽ:
Có \(\overrightarrow {AB} = \left( {3 - 1;3 - 2;4 - 3} \right) = \left( {2;1;1} \right)\) và \(\overrightarrow {AC} = \left( { - 1 - 1;1 - 2;2 - 3} \right) = \left( { - 2; - 1; - 1} \right)\).
Nhận thấy \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là hai vectơ đối nhau.
Trong không gian với hệ tọa độ $Oxyz$, cho ba vectơ \(\vec a = \left( {3; - 1; - 2} \right),\vec b = \left( {1;2;m} \right)\) và \(\vec c = \left( {5;1;7} \right)\). Giá trị \(m\) bằng bao nhiêu để \(\vec c = \left[ {\vec a,\vec b} \right]\).
Ta có: \(\left[ {\vec a,\vec b} \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\2&m\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&3\\m&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}3&{ - 1}\\1&2\end{array}} \right|} \right) = \left( { - m + 4; - 2 - 3m;7} \right)\)
\(\vec c = \left[ {\vec a,\vec b} \right] \Leftrightarrow \left\{ \begin{array}{l} - m + 4 = 5\\ - 2 - 3m = 1\\7 = 7\end{array} \right. \Leftrightarrow m = - 1\)
